Математика / Курсовая работа: Линейное и нелинейное программирование

Курсовая работа: Линейное и нелинейное программирование

3.1.2 Метод поиска по координатной сетке с постоянным шагом и метод случайного поиска. Сравнение результатов вычислений

Метод поиска глобального минимума, называемый методом поиска по координатной сетке, является надежным, но применим только для задач малой размерности (n<4). Неправильный выбор начального шага сетки может привести к тому, что в действительности один из локальных минимумов может быть принят как глобальный. Из всех значений целевой функции, вычисленных в узлах координатной сетки, выбирается минимальное. Результат: число испытаний 905, f(X^* ) = -2.500, X^* =(-0.500; 2.000)

Метод случайного поиска характеризуется намеренным введением элемента случайности в алгоритм поиска. Этот метод предполагает наличие генератора случайных чисел, обращаясь к которому, в любой нужный момент времени можно получить реализацию случайного вектора с заданным законом распределения. Результат: число испытаний 299, f(X^* ) = -2.469, X^* =(-0.677; 2.173).

Расчет в системе MathCAD: f(X^* ) = -2.500, X^* =(-0.500; 2.000)

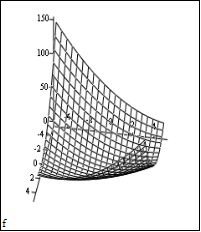
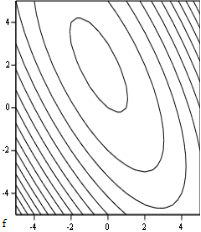
Как видим, метод случайного поиска сократил число испытаний на 66%, при этом относительная погрешность составляет 1%. Т.е. мы достигли значительного сокращения вычислений с небольшой относительной погрешностью.

3.2 Задача одномерной оптимизации функции

3.2.1 Постановка задачи одномерной оптимизации функции

Задание для нахождения одномерного локального экстремума функции (одномерная оптимизация) состоит в том, чтобы выполнить поиск минимума заданной функции методом дихотомии (3-4 итерации), уточнить интервал поиска методом Фибоначчи (3 итерации) и завершить поиск методом кубической аппроксимации.