Курсовая работа: Линейное и нелинейное программирование
F = -F’ = 6 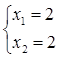
2.2.3 Метод ветвей и границ
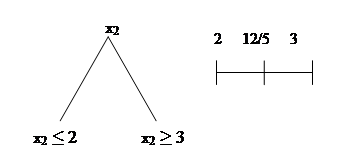 | b | x1 | x2 |
| x3 |
12/5 | -1/5 | 2/5 |
| x4 |
19/10 | 3/10 | -1/10 |
| F’ |
-31/5 | -2/5 | -1/5 |
Задача № 1
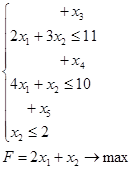
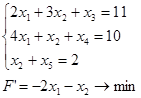
Приводим к каноническому виду:
x3 , x4 , x5 – базисные переменные, x1 , x2 – свободные переменные
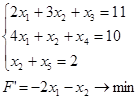
| ↑ | |||||
| b | x1 | x2 | |||
| x3 | 11 | 2 | 3 | 11/2 | |
| -5 | -1/2 | -1/2 | |||
| ← | x4 | 10 | 4 | 1 | 5/2 |
| 5/2 | 1/4 | 1/4 | |||
| x5 | 2 | 0 | 1 | ||
| 0 | 0 | 0 | |||
| F’ | 0 | 2 | 1 | ||
| -5 | -1/2 | -1/2 | |||
| ↑ | |||||
| b | x4 | x2 | |||
| x3 | 6 | -1/2 | 5/2 | 12/5 | |
| -5 | 0 | -5/2 | |||
| x1 | 5/2 | 1/4 | 1/4 | 10 | |
| -1/2 | 0 | -1/4 | |||
| ← | x5 | 2 | 0 | 1 | 2 |
| 2 | 0 | 1 | |||
| F’ | -5 | -1/2 | 1/2 | ||
| -1 | 0 | -1/2 | |||
| b | x4 | x5 | |||
| x3 | 1 | -1/2 | -5/2 | ||
| x1 | 2 | 1/4 | -1/4 | ||
| x2 | 2 | 0 | 1 | ||
| F’ | -6 | -1/2 | -1/2 | ||
X = (2, 2, 1, 0, 0)
F’ = -6
F = -F’ = 6 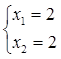
Задача № 2
Решаем задачу с x2 ≥ 3 в подсистеме «Поиск решения» системы Excel. Получаем допустимое не оптимальное решение F = 5, X = (1, 3)
| =2*$B$1+$B$2 | 1 | =2*$B$1+3*$B$2 | 11 |
| 3 | =4*$B$1+$B$2 | 10 | |
| =$B$2 | 3 |
| 5 | 1 | 11 | 11 |
| 3 | 7 | 10 | |
| 3 | 3 |
| Ограничения | |||||
| Ячейка | Имя | Значение | Формула | Статус | Разница |
| $C$1 | 11 | $C$1<=$D$1 | связанное | 0 | |
| $C$2 | 7 | $C$2<=$D$2 | не связан. | 3 | |
| $C$3 | 3 | $C$3>=$D$3 | связанное | 0 | |
2.3 Задача целочисленного линейного программирования с булевскими переменными
2.3.1 Постановка задачи целочисленного линейного программирования с булевскими переменными
Составить самостоятельно вариант для задачи целочисленного линейного программирования с булевскими переменными с учетом следующих правил: в задаче используется не менее 5 переменных, не менее 4 ограничений, коэффициенты ограничений и целевой функции выбираются произвольно, но таким образом, чтобы система ограничений была совместна. Задание состоит в том, чтобы решить ЗЦЛП с булевскими переменными, используя алгоритм Баллаша и определить снижение трудоемкости вычислений по отношению к решению задачи методом полного перебора.
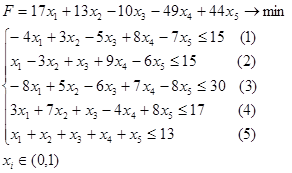
2.3.2 Метод Баллаша
| № | x4 | x3 | x2 | x1 | x5 | Выполнение ограничений | Значение F | |||||
| 0 | 1 | 2 | 3 | 4 | 5 | |||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | Fф=0 | |||||
| 2 | 0 | 0 | 0 | 0 | 1 | 44 | ||||||
| 3 | 0 | 0 | 0 | 1 | 0 | 17 | ||||||
| 4 | 0 | 0 | 0 | 1 | 1 | 61 | ||||||
| 5 | 0 | 0 | 1 | 0 | 0 | 13 | ||||||
| 6 | 0 | 0 | 1 | 0 | 1 | 57 | ||||||
| 7 | 0 | 0 | 1 | 1 | 0 | 30 | ||||||
| 8 | 0 | 0 | 1 | 1 | 1 | 74 | ||||||
| 9 | 0 | 1 | 0 | 0 | 0 | -10 | + | + | + | + | + | Fф=-10 |
| 10 | 0 | 1 | 0 | 0 | 1 | 34 | ||||||
| 11 | 0 | 1 | 0 | 1 | 0 | 7 | ||||||
| 12 | 0 | 1 | 0 | 1 | 1 | 51 | ||||||
| 13 | 0 | 1 | 1 | 0 | 0 | 3 | ||||||
| 14 | 0 | 1 | 1 | 0 | 1 | 47 | ||||||
| 15 | 0 | 1 | 1 | 1 | 0 | 20 | ||||||
| 16 | 0 | 1 | 1 | 1 | 1 | 64 | ||||||
| 17 | 1 | 0 | 0 | 0 | 0 | -49 | + | + | + | + | + | Fф=-49 |
| 18 | 1 | 0 | 0 | 0 | 1 | -5 | ||||||
| 19 | 1 | 0 | 0 | 1 | 0 | -32 | ||||||
| 20 | 1 | 0 | 0 | 1 | 1 | 12 | ||||||
| 21 | 1 | 0 | 1 | 0 | 0 | -36 | ||||||
| 22 | 1 | 0 | 1 | 0 | 1 | 8 | ||||||
| 23 | 1 | 0 | 1 | 1 | 0 | -19 | ||||||
| 24 | 1 | 0 | 1 | 1 | 1 | 25 | ||||||
| 25 | 1 | 1 | 0 | 0 | 0 | -59 | + | + | + | + | + | Fф=-59 |
| 26 | 1 | 1 | 0 | 0 | 1 | -15 | ||||||
| 27 | 1 | 1 | 0 | 1 | 0 | -42 | ||||||
| 28 | 1 | 1 | 0 | 1 | 1 | 2 | ||||||
| 29 | 1 | 1 | 1 | 0 | 0 | -46 | ||||||
| 30 | 1 | 1 | 1 | 0 | 1 | -2 | ||||||
| 31 | 1 | 1 | 1 | 1 | 0 | -29 | ||||||
| 32 | 1 | 1 | 1 | 1 | 1 | 15 | ||||||
Фильтрующее ограничение:
![]()
2.3.3 Определение снижения трудоемкости вычислений
Решение задачи методом полного перебора составляет 6*25 =192 вычисленных выражения. Решение задачи методом Баллаша составляет 3*6+(25 -3)=47 вычисленных выражений. Итого снижение трудоемкости вычислений по отношению к решению задачи методом полного перебора составляет ![]() .
.
3 Нелинейное программирование
3.1 Задача поиска глобального экстремума функции
3.1.1 Постановка задачи поиска глобального экстремума функции
Необходимо написать программа для поиска экстремума функции. Задание состоит в следующем: 1) найти точку глобального экстремума функции f( X) методом поиска по координатной сетке с постоянным шагом; 2) найти точку глобального экстремума функции f( X) методом случайного поиска; 3)сравнить результаты вычислений.