Курсовая работа: Математические методы в решении экономических задач
Общий вид задачи линейного программирования:
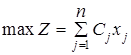
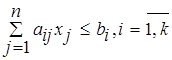
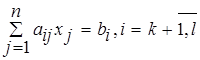
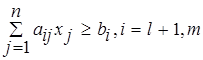
![]() ,
,![]()
Ограничения:
1. Правые части всех ограничений должны быть неотрицательными ![]() . Если какой-нибудь из коэффициентов
. Если какой-нибудь из коэффициентов ![]() < 0, то необходимо коэффициенты ограничения слева и справа домножить на "-1" и изменить знак данного ограничения на противоположный;
< 0, то необходимо коэффициенты ограничения слева и справа домножить на "-1" и изменить знак данного ограничения на противоположный;
2. Все ограничения должны быть представлены в виде равенств, поэтому при переходе от неравенства к равенству используют аппарат дополнительных переменных.
Если исходные ограничения определяют расход некоторого ресурса (знак "![]() "), то переменные
"), то переменные
![]()
следует интерпретировать как остаток, или неиспользованную часть ресурса. В этом случае ![]() – остаточная переменная и вводится в уравнение со знаком "+". Если исходные ограничения определяют избыток некоторого ресурса (знак "
– остаточная переменная и вводится в уравнение со знаком "+". Если исходные ограничения определяют избыток некоторого ресурса (знак "![]() "), то вводится избыточная переменная
"), то вводится избыточная переменная
![]()
знаком "-".
Переменные:
Все переменные должны быть неотрицательными, т.е.
![]() .
.
Если переменная не имеет ограничения в знаке, то её нужно представить как разность двух неотрицательных переменных:
![]() ,
,
где ![]() . Такую подстановку следует использовать во всех ограничениях, содержащих эту переменную, а также в выражении для целевой функции.
. Такую подстановку следует использовать во всех ограничениях, содержащих эту переменную, а также в выражении для целевой функции.
Если такая переменная попадает в оптимальное решение, то ![]() .
.
Целевая функция:
Целевая функция задачи линейного программирования есть уравнение плоскости (или гиперплоскости для числа переменных больше трех). Максимальное или минимальное значение целевая функция задачи линейного программирования достигает либо в вершине выпуклого многогранника, либо на одной из его граней. Таким образом, решение (решения) задачи линейного программирования лежит в вершинах выпуклого многогранника и для его нахождения надо вычислить значения целевой функции в вершинах выпуклого многогранника, определяемого условиями-ограничениями задачи.
Приступаем к решению задачи.
Требуется составить план производства изделий А₁ и А₂ обеспечивающий максимальную прибыль предприятия от реализации готовой продукции. Необходимо:
Решить задачу геометрически;
Решить задачу симплекс-методом(аналитическим и табличным)
Сформулировать двойственную задачу и найти её решение.
Задача №1