Курсовая работа: Математические методы в решении экономических задач

Занесём необходимые нам данные во вспомогательную таблицу:

Вид сырья	Продукция		Ограничения по сырью
	А₁	А₂
1-й	5	2	750
2-й	4	5	807
3-й	1	7	840
прибыль	30	49

Решение:

Предположим, что будет изготовлено Х₁ единиц изделий вида А₁ и Х₂ единиц - вида А₂. Поскольку производство продукции ограничено имеющимися в распоряжении предприятия сырьем каждого вида и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства:

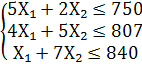
Общая прибыль от реализации Х₁ изделий А₁ и Х₂ изделий вида А₂ составит

F = 30Х₁ +49Х₂.

Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.

Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые: