Курсовая работа: Математические модели поведения производителей

max F(x), wx С, х 0.

Составим функцию Лагранжа:

L(x,) = F(x) + (C-wx),

L(x,)= +;

Дифференцируя заданную функцию по перменным х₁ , х₂ , х₃ , имеем систему неравенств:

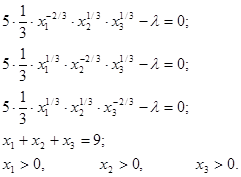
Решая систему, получим значения: при =4,061 , 0,877 .

Обозначим найденую точку через М . Найдем значение функции Х в полученой точке:

11,28.

Найдем предельные продукты по ресурсам в точке М :

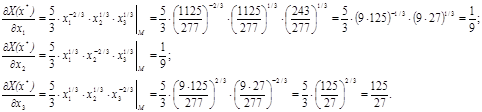
2. Производственная функция фирмы имеет следующий вид:

Х =3.

Определить предельные продукты по ресурсам и построить изокванту Х =3. Написать уравнеие изоклинали (линии наибольшего роста выпуска), проходящей через точку х₁ =1, х₂ =1 , найти норму замены первого ресурса вторым в этой точке.

Решение.

Предельным продуктом по первому ресурсу является

по второму –

Уравнение изокванты имеет вид при Х =3 :

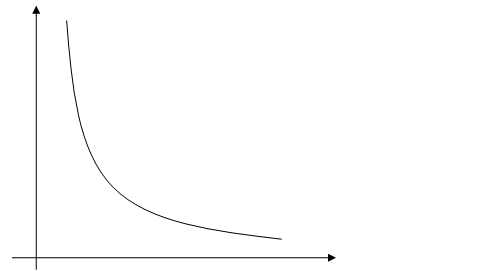х₁

х₂

Общее уравнение изоклинали имеет вид: 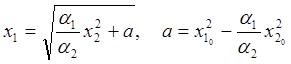, где (х_{1 0} , х_{2 0} ) – координаты точки, через которую проходит изоклиналь. Подставим точки в уравнение, получим: .

Норма замены первого ресурса вторым в этой точке равен:

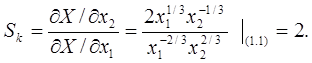
Список используемой литературы

1. В. А. Колемаев «Математическая экономика».

2. В. Д. Камаев «Экономическая теория для вузов».

3. В. С. Немчинов «Экономико-математические методы и модели».