Курсовая работа: Метод Крамера

1.1 Постановка задачі

Нехай дано систему п лінійних алгебраїчних рівнянь з п змінними

(I=1.2…..n) (1)

Систему (1) можна записати у вигляді одного матричного рівняння

AX=B, (2)

де

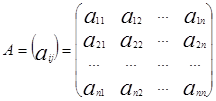
матриця коефіцієнтів (індекс і вказує рівняння, якому належить коефіцієнт, а індекс j – змінну, при якій він стоїть),

,

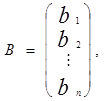
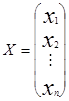відповідно стовпець вільних членів і стовпець змінних.

Упорядкована сукупність п чисел , яка, будучи підставленою в систему (1) замість , перетворює всі рівняння в правильні числові рівності, називається розв’язком системи (1)

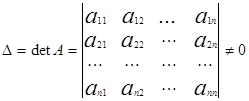
то вона має єдиний розв’язок. Його можна обчислити за формулами Крамера.

(k=1,2,…,n),

де матрицю дістають з матриці А, замінивши її k-й стовпець стовпцем вільних членів.

Методи розв’язування систем лінійних рівнянь можна поділити на дві групи: точні й ітераційні.

Точними називають такі методи, які дають змогу знайти точний розв’язок системи (1) за допомогою виконання скінченої кількості арифметичних операцій у припущенні, що всі обчислення виконуються точно (без округлень), а коефіцієнти системи і вільні члени – точні числа. Але на практиці всі обчислення виконуються з обмеженою кількістю десяткових розрядів, а ірраціональні коефіцієнти і вільні члени, якщо такі є, замінюються раціональними числами. Тому в процесі обчислення вдаються до округлень, а це означає, що розв’язки, які обчислюються за точними методами, фактично є наближеними числами з певними похибками (похибками округлень). До точних належать метод Гаусса, метод квадратних коренів, правило Крамера тощо.

Інтераційними називають такі методи, які дають змогу знайти наближений розв’язок системи (1) із заздалегідь вказаною точністю шляхом виконання скінченої кількості арифметичних операцій, хоч самі обчислення можуть проводитись і без округлень, а коефіцієнти і вільні члени системи бути точними числами. Точний розв’язок системи (1) за допомогою ітераційних методів може знайти тільки теоретично як границю збіжного нескінченного процесу. Розв’язуючи системи рівнянь ітераційними методами, крім похибок округлення, треба враховувати похибку методу. До ітераційних належать метод ітерації, метод Зейделя тощо.

В завданні на курсовий проект передбачено розробку програмного забезпечення для розв’язування системи лінійних рівнянь за формулами Крамера.

Програма повинна забезпечувати виконання таких операцій:

ввід коефіцієнтів системи рівнянь та вільних членів;

обчислення визначників системи та знаходження розв’язків системи;

вивід систем рівнянь та її розв’язків на екран.

Для реалізації поставленого завдання в середовищі Turbo Pascal 7.0 розроблено програму KRAMER.PAS. Перелічені вище операції реалізуються в програмі за допомогою процедур.

1.2 Методи розв’язування задачі

Розглянемо систему трьох лінійних рівнянь з трьома невідомими:

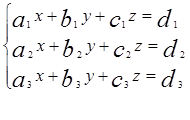(1)

Систему (1) можна також записати так:

, і=1, 2, 3.