Курсовая работа: Метод квадратных корней для симметричной матрицы при решении систем линейных алгебраических уравнений
на тему: «Метод квадратных корней для симметричной матрицы при решении СЛАУ»
Новосибирск, 2010
Содержание
Введение
1. Математическая постановка задачи
2. Описание программного обеспечения
3. Описание тестовых задач
4. Анализ результатов. Выводы
Заключение
Список использованной литературы
Введение
В данной работе мы будем исследовать метод квадратных корней для симметричной матрицы при решении систем линейных алгебраических уравнений (СЛАУ).
В жизни, очень часто приходится описывать состояние различных объектов, в том числе и экономических с помощью математических моделей. После того, как объект описан такой моделью, очень часто необходимо найти его состояние равновесия.
Именно тогда, чтобы найти это состояние, приходится решать систему алгебраических уравнений. В нашем случае система состоит из n линейных уравнений с n неизвестными, и ее можно описать так:
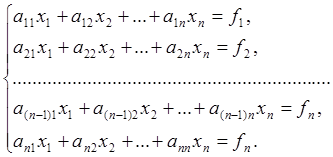
Также данную систему можно записать и в матричном виде:
Тогда мы будем иметь матрицу коэффициентов А:
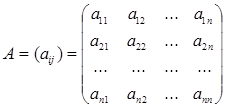 ,
,
столбец свободных членов уравнений f:
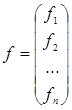 ,
,
и столбец неизвестных х:
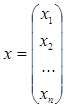 .
.
Чтобы данная СЛАУ имела единственное решение, нужно, чтобы определитель матрицы коэффициентов А не был равен нулю (det(A))¹0.
Данную систему можно решить многими методами. Например, методом Гаусса. Решение этой системы методом Гаусса потребует выполнить
![]() действий,
действий,
где n – число неизвестных в уравнении. А это довольно таки трудоемко, особенно при больших порядках числа n.
Еще одним точным методом для решения данных СЛАУ является рассматриваемый в данной работе метод квадратных корней для симметричной матрицы А.
Изучать данный метод мы будем следующим образом. Сначала рассмотрим математическую постановку задачи для метода квадратных корней при решении СЛАУ. В данном разделе будет полностью описана математическая модель метода. Затем рассматривается разработанная реализация данного метода в среде MatLab 7.0. После того, как метод будет реализован, можно провести анализ точности этого метода. Анализ будет основываться на исследовании влияния мерности матрицы А, ее обусловленности, разреженности на точность полученного решения. По результатам исследования будет приведен график зависимости точности полученного решения от мерности матрицы А.
метод решение корень симметричная матрица
1. Математическая постановка задачи
Метод квадратных корней используется для решения линейной системы вида Ах=f(1.1), в которой матрица А является симметричной, т.е. аij =aji , где (i, j = 1, 2, …, n).
Данный метод является более экономным и удобным по сравнению с решением систем общего вида. Решение системы осуществляется в два этапа.
Прямой ход . Представим матрицу А в виде произведения двух взаимно транспонированных треугольных матриц:
А = Т¢ Т, (1.2)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--