Курсовая работа: Метод Монте Карло и его применение
writeln(‘s=’,s); {Сумма функции для n произвольных значений}
Integral:=(1/n)*k*s ;
writeln(‘Интеграл=’,Integral);
readln;
END.
Требуется ввести промежуток интегрирования и количество испытаний, интегрируемая функция уже задана в программе (но ее можно поменять).
; 
.
|
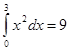Функция |
k |
N=10 |
N=100 |
N=500 |
N=1000 |
|
f(x)=1+x |
2 |
5.737 |
5.9702 |
6.02 |
5.99 |
|
f(x)=x*x |
3 |
9.6775 |
8.528 |
8.7463 |
8.937 |
§7. Вычисление кратных интегралов методом Монте-Карло.
Пусть функция 
непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл
. (1)
Геометрически число I представляет собой (m+1)-мерный объём прямого цилиндроида в пространстве 
, построенного на основании S и ограниченного сверху данной поверхностью 
, где 
.