Курсовая работа: Метод наименьших квадратов 2

Пусть имеется выборка Z_n =col(X₁ ,…X_n ) с реализацией z_n =(x₁ ,…x_n ).

Определение 2.2. Точечной (выборочной ) оценкой неизвестного параметра распределения Ө ΘIR^s называется произвольная статистика (Z_n ), построенная по выборке Z_n и принимающая значения в множестве Θ.

Замечание 2.1. Реализацию (z_n ) оценки (Z_n ), принимают, как правило, за приближенное значение неизвестного параметра Ө .

Ясно, что существует много разных способов построения точечной оценки которые учитывают тип статистической модели. Для параметрической и не параметрической моделей эти способы могут быть различны. Рассмотрим некоторые свойства, которые характеризуют качество введенной оценки.

Определение 2.3. Оценка (Z_n ) параметра Ө называется несмещенной , если ее МО равно Ө , т.е. M[(Z_n )]= Ө для любого Ө Θ.

Определение 2.4. Оценка (Z_n ) параметра Ө называется состоятельной, если она сходится по вероятности к Ө , т.е. (Z_n ) Ө при n → ∞ для любого Ө Θ.

Определение 2.5. Оценка (Z_n ) параметра Ө называется сильно состоятельной , если она сходится почти наверное к Ө , т.е. (Z_n ) Ө при n → ∞ для любого Ө Θ.

Определение 2.6. Несмещенная оценка *(Z_n ) скалярного параметра Ө называется эффективной , если D[*(Z_n )]≤ D[(Z_n )] для всех несмещенных оценок (Z_n ) параметра Ө , т.е. ее дисперсия минимальна по сравнению с дисперсиями других несмещенных оценок при одном и том же объеме n выборки Z_n .

Вообще говоря, дисперсии несмещенных оценок могут зависеть о параметра Ө. В этом случае под эффективной оценкой понимается такая, для которой вышеприведенное неравенство является строгим хотя бы для одного значения параметра Ө.

3.Интервальные оценки.

Пусть имеется параметрическая статистическая модель (S_Ө , F_Zn ( z_n ,Ө )), Ө ΘIR¹ , и по выборке Z_n =col(X₁ ,…X_n ), соответствующей распределению F( x,Ө ), наблюдаемой СВ X, требуется оценить неизвестный параметр Ө . Вместо точечных оценок, рассмотренных ранее, рассмотрим другой тип оценок неизвестного параметра Ө ΘIR¹ .

Определение 3.1. Интервал [θ₁ (Z_n ),θ₂ (Z_n )] со случайными концами, «накрывающий» с вероятностью 1-α, 0<α<1, неизвестный параметр θ, т.е.

P{ θ₁ (Z_n )≤ θ ≤ θ₂ (Z_n )}= 1-α,

называется доверительным интервалом (или интервальной оценкой ) уровня надежности 1-α параметра θ.

Аналогично определяется доверительный интервал для произвольной функции от параметра θ.

Определение 3.2. Число δ=1-α называется доверительной вероятностью или уровнем доверия (надежности).

Определение 3.3. Доверительный интервал [θ₁ (Z_n ),θ₂ (Z_n )] называется центральным , если выполняются следующие условия:

P{ θ≥ θ₂ (Z_n )}= , P{ θ₁ (Z_n ) ≥ θ}=.

Часто вместо двусторонних доверительных интервалов рассматривают односторонние доверительные интервалы, полагая θ₁ (Z_n )= -∞ или θ₂ (Z_n )= +∞.

Определение 3.4. Интервал, границы которого удовлетворяют условию:

P{ θ≥ θ₂ (Z_n )}= α (или P{ θ₁ (Z_n ) ≥ θ}= α.),

называется соответственно правосторонним ( или левосторонним) доверительным интервалом.

4.Проверка статистических гипотез.

Определение 4.1. Статистической гипотезой H или просто гипотезой называется любое предположение относительно параметров ли законов распределения СВ X, проверяемое по выборке Z_n .

Определение 4.2. Проверяемая гипотеза называется основной ( или нулевой ) и обозначается Ho. Гипотеза, конкурирующая с H_o , называется альтернативной и обозначается H₁ ,

Определение 4.3. Статистическая гипотеза Ho называется простой, если она однозначно определяет параметр или распределение СВ X. В противном случае гипотеза H_o называется сложной.

Определение 4.4. Статистическим критерием (критерием согласия, критерием значимости или решающим правилом) проверки гипотезы H_o называется правило, в соответствии с которым по реализации z=φ(z_n ) статистики Z гипотеза H_o принимается или отвергается.

Определение 4.5. Критической областью статистического критерия называют область реализации z статистики Z, при которых гипотеза Ho отвергается.

Определение 4.6 . Доверительной областью G статистического критерия называется область значений z статистики Z, при которых гипотеза H_o принимается.

Например, в качестве статистического критерия можно использовать правило:

1. Если значение z= φ(z_n ) статистики Z= φ(z_n ) лежит в критической области 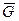, то гипотеза Ho отвергается и принимается альтернативная гипотеза H₁ ;
2. Если реализация z= φ(z_n ) статистики Z= φ(z_n ) лежит в доверительной области G, то гипотеза H_o принимается.

При реализации этого правила возникают ошибки двух видов.

Определение 4.7 . Ошибкой 1-го рода называется событие, состоящее в том, что гипотеза H_o отвергается, когда она верна.

Определение 4.8 . Ошибкой 2-го рода называется событие, состоящее в том, что принимается гипотеза H_o , когда верна гипотеза H₁ .

Определение 4.9 . Уровнем значимости статистического критерия называется вероятность ошибки 1-го рода α=P{Z|H_o }, Вероятность ошибки 1-го рода α может быть вычислено, если известно распределение F(z|H_o ) статистики Z.