Курсовая работа: Метод наименьших квадратов 2
Дата сдачи КР
Проверил курсовую работу
Шин Галина Захаровна
Москва 2005
Оглавление
1. Исходные данные………………………………………………….3
2. Постановка задачи…………………………………………………4
3. Теоретическая часть……………………………………………….5
4. Расчетная часть……………………………………………………10
5. График …………………………………………………………….16
6. Приложение………………………………………………………..17
7. Список литературы……………………………………………… 18
1.Исходные данные
| Номер | Время X | Величина Y |
| 1 | -1 | 6,323 |
| 2 | -0,95 | -22,817 |
| 3 | -0,9 | -24,908 |
| 4 | -0,85 | 20,708 |
| 5 | -0,8 | 9,145 |
| 6 | -0,75 | -1,283 |
| 7 | -0,7 | 39,694 |
| 8 | -0,65 | -16,954 |
| 9 | -0,6 | 29,198 |
| 10 | -0,55 | -43,22 |
| 11 | -0,5 | 11,371 |
| 12 | -0,45 | -5,745 |
| 13 | -0,4 | 11,171 |
| 14 | -0,35 | 1,058 |
| 15 | -0,3 | -15,19 |
| 16 | -0,25 | -45,976 |
| 17 | -0,2 | -0,25 |
| 18 | -0,15 | -18,76 |
| 19 | -0,1 | 14,7 |
| 20 | -0,05 | -17,959 |
| 21 | 0 | -0,377 |
| 22 | 0,05 | -12,988 |
| 23 | 0,1 | 55,728 |
| 24 | 0,15 | -2,009 |
| 25 | 0,2 | -4,523 |
| 26 | 0,25 | -11,937 |
| 27 | 0,3 | -17,419 |
| 28 | 0,35 | 1,564 |
| 29 | 0,4 | 12 |
| 30 | 0,45 | -25,92 |
| 31 | 0,5 | 29,946 |
| 32 | 0,55 | -27,554 |
| 33 | 0,6 | -6,12 |
| 34 | 0,65 | -5,25 |
| 35 | 0,7 | -7,488 |
| 36 | 0,75 | -29,674 |
| 37 | 0,8 | -34,196 |
| 38 | 0,85 | -0,239 |
| 39 | 0,9 | 4,966 |
| 40 | 0,95 | -5,11 |
| 41 | 1 | -7,541 |
Постановка задачи
- а).Задано множество пар значений {(xt ,yt )}, t=
(n=41), представляющих собой результаты измерений функции. Дан прибор, который генерирует функцию y(x)=ax+b. На вход поступает сигнал x1 ,x2 ,..,xn ; на выходе: y1 ,y2 ,…,yn .Числа не соответствуют внутренним числам, так как прибор имеет шумы
yt =axt +b +εt , t=,
где a,b – неизвестные коэффициенты, а εt – независимые в совокупности случайные величины с нормальным законом распределения: εt ~N(0,σ2 ), где σ2 неизвестная дисперсия; 0 – математическое ожидание шума εt . М εt =0, D εt = σ2 .
Требуется найти методом наименьших квадратов неизвестные параметры кривой регрессии.
y(x)=ax+b– кривая регрессии – условное матожидание случайной величины Y при аргументе x, М(y/x).
б). Построить график линии регрессии ỹ(x).
- Найти точечную оценку для неизвестного параметра
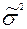неизвестной дисперсии σ2 , которая входит в нормальный закон распределения. - Построить интервальные оценки для неизвестных коэффициентов a,b и дисперсии σ2 на уровне доверия j1 =0,9; j2 =0,95.
- С помощью критерия Снедекера-Фишера проверить гипотезу Ho : a=0 и гипотезу Ho : b=0 на уровне доверия j1 =0,9 и j2 =0,95.
Теоретическая часть
1.Выборка.
Математическая статистика – наука о математических методах, позволяющих по статистическим данным, например по реализациям случайной величины (СВ), построить теоретико-вероятностную модель исследуемого явления. Задачи математической статистики являются, в некотором смысле, обратными к задачам теории вероятностей. Центральным понятием математической статистики является выборка.
Определение 1. Однородной выборкой (выборкой) объема n при n
1 называется случайный вектор Zn =col(X1 ,…,Xn ), компоненты которого Xi , i=
, называемые элементами выборки, являются независимыми СВ с одной и той же функцией распределения F(x). Будем говорить, что выборка Zn соответствует функции распределения F(x).
Числа, данные, полученные после опыта – апостериорная выборка.
Определение 2. Реализацией выборки называется неслучайный вектор zn =col(x1 ,…,xn ), компонентами которого являются реализации соответствующих элементов выборки Xi , i=.
Из этих определений вытекает, что реализацию выборки zn можно также рассматривать как последовательность x1,…,xnиз n реализаций одной и той же СВ X, полученных в серии из nнезависимых одинаковых опытов, проводимых в одинаковых условиях. Поэтому можно говорить, что выборка Zn порождена наблюдаемой СВ X, имеющей распределение Fx (x)=F(x).
Определение 3. Если компоненты вектора Zn независимы, но их распределения F1 (x1 ),…,Fn (xn ) различны, то такую выборку называют неоднородной.
Определение 4. Множество Sвсех реализаций выборки Zn называется выборочным пространством.
Выборочное пространство может быть всем n-мерным евклидовым пространством Irn или его частью, если СВ X непрерывна, а также может состоять из конечног или счетного числа точек из Irn, если СВ X дискретна.
На практике при исследовании конкретного эксперимента распределения F1 (x1 ),…,Fn (xn ) СВ X1 ,…,Xn редко бывают известны полностью. Часто априори (до опыта) можно лишь утверждать, что распределение FZn (zn )=F1 (x1 ),…Fn (xn ) случайного вектора Zn принадлежит некоторому классу (семейству) F.
Определение 5. Пара (S,F) называется статистической моделью описания серии опытов, порождающих выборку Zn .
Определение 6. Если распределение FZn (zn ,Ө ) из класса F определены с точностью до некоторого векторного параметра Ө 
Θ
IRs , то такая статистическая модель называется параметрической и обозначается (SӨ , FZn ( zn , Ө )), Ө ΘIRs .
В некоторых случаях выборочное пространство может не зависеть от неизвестного параметра Ө распределения FZn (zn ,Ө ).
В зависимости от вида статистической модели в математической статистике формулируются соответствующие задачи по обработке информации, содержащейся в выборке.
Определение 7. СВ Z=φ(Zn ), где φ(Zn ) – произвольная функция, определенная на выборочном пространстве S и не зависящая от распределения FZn (zn ,Ө ), называется статистикой.
2. Точечные оценки.
Определение 2.1. Параметром распределения Ө ΘIR1 СВ X называется любая числовая характеристика этой СВ ( математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции распределения.
В общем случае будем предполагать, что параметр распределения Ө может быть векторным, т.е. Ө ΘIRs .
--> ЧИТАТЬ ПОЛНОСТЬЮ <--