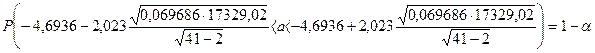Курсовая работа: Метод наименьших квадратов 2

.

2.Построим интервальные оценки дисперсии s² на уровне доверия g=0,9:

a=1-g=0,1,

Далее, 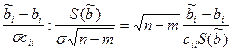~t(n-m),

где c_ii обозначает (i,i)-ый элемент матрицы А^-1 , а символ t(n-m) – распределение Стьюдента с n-m степенями свободы. Отсюда

,

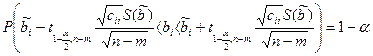где - квантиль уровня для распределения Стьюдента с n степенями свободы.

Квантили распределения Стьюдента для интервалов a,b:

а). ,

б). ,

,

,

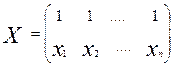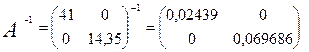
С₁₁ =0,02439 (для свободного члена,b), С₂₂ =0,069686 (для a).

n=41,

m=2.

II.1. Построим интервальную оценку для коэффициента b на уровне доверия g=0,95:

,

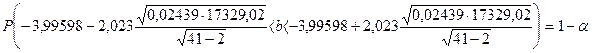
2. Построим интервальную оценку для коэффициента b на уровне доверия g=0,9:

,

.

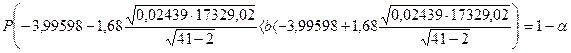
III. 1. Построим интервальную оценку для коэффициента a на уровне доверия g=0,95:

,