Курсовая работа: Метод Ньютона для решения нелинейных уравнений
x* О [c,b] , если f(с)Ч f(а) > 0 ;
x* О [a,c] , если f(c)Ч f(b) < 0 .
Если f'(x) не меняет знак на [a,b], то обозначая c=x1 и считая начальным приближением a или b получим итерационные формулы метода хорд с закрепленной правой или левой точкой.
x0 =a, xi+1 = xi - f(xi )(b-xi ) / (f(b)-f(xi ), при f '(x)Ч f "(x) > 0 ;
x0 =b, xi+1 = xi - f(xi )(xi -a) / (f(xi )-f(a), при f '(x)Ч f "(x) < 0 .

Сходимость метода хорд линейная.
1.2 Алгоритм метода Ньютона
Построим эффективный алгоритм вычисления корней уравнения. Пусть задано начальное приближение ![]() . Вычислим в этой точке значение функции
. Вычислим в этой точке значение функции ![]() и её производной
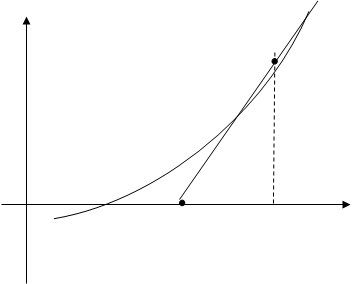
и её производной ![]() . Рассмотрим графическую иллюстрацию метода:
. Рассмотрим графическую иллюстрацию метода:
![]() .
.
Далее получим следующее приближение в точке ![]() , проводя касательную из точки (
, проводя касательную из точки (![]() ) до пересечения с осью абсцисс:
) до пересечения с осью абсцисс:
![]() (8)
(8)
Продолжая этот процесс, получим известную формулу Ньютона:
![]() (9)
(9)
y ![]()
![]()
![]() x
x
Рис. 1.
Приведем простейшую рекурсивную подпрограмму-функцию:
function X_Newt(x,eps:real):real;
var y:real;
begin
y:=x-f(x)/f1(x);
if abs(f(x)) > eps
then X_Newt:=X_Newt(y,eps)
else X_Newt:=y
end;
Метод Ньютона (касательных) характеризуется квадратичной скоростью сходимости, т.е. на каждой итерации удваивается число верных знаков. Однако этот метод не всегда приводит к нужному результату. Рассмотрим этот вопрос подробнее.
Преобразуем уравнение (1) к эквивалентному уравнению вида:
x=g(x) (10)