Курсовая работа: Метод Ньютона для решения нелинейных уравнений

Пример 5

Решить уравнение методом Ньютона.

-2+e^x - e^-x =0.

Решение:

Вычислим первую производную функции.

F’(x) = e^x +e^-x .

Теперь вычислим вторую производную от функции.

F’’(x) = e^x -e^-x .

Построим приближённый график данной функции.

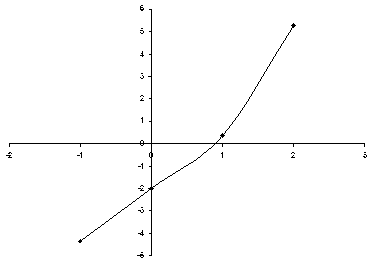
Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x⁽⁰⁾ ) * f’’(x⁽⁰⁾ ) > 0.

Пусть x⁽⁰⁾ = 1, тогда f(2)*f’’(2) = 0. 350 * 2, 350 = 0. 823 > 0,

Условие выполняется, значит берём x⁽⁰⁾ = 1.

Теперь составим таблицу значений, для решения данного уравнения.

k	x(k)	f(x(k))	f’(x(k))	| x(k+1) - x(k) |
0	1, 000	0, 350	3, 086	0, 114
1	0, 886	0, 013	2, 838	0, 005
2	0, 881	0, 001	2, 828	0, 000
3	0, 881

Отсюда следует, что корень уравнения х = 0, 881.

III. Разработка программного продукта

3.1 Описание программы

Данная программа создана для работы в текстовом и графическом режиме. Она состоит из модуля Graph, Crt, трёх функций и трёх процедур.

1. модуль Crt предназначен для обеспечения контроля над текстовыми режимами экрана, расширенными кодами клавиатуры, цветами, окнами и звуком;

2. модуль Graph предназначен для обеспечения контроля над графическими объектами;

3. procedure GrafInit - инициализирует графический режим;

4. function VF – вычисляет значение функции;

5. function f1 – вычисляет значение первой производной функции;

6. function X_Newt – реализует алгоритм решения уравнения методом Ньютона.

7. procedure FGraf – реализует построение графика заданной функции f(x);

Ots=35 - константа, определяющая количество точек для отступа от границ монитора;

fmin, fmax – максимальные и минимальные значения функции;

SetColor(4) – процедура, которая устанавливает текущий цвет графического объекта, используя палитру, в данном случае это красный цвет;

SetBkColor(9) – процедура, которая устанавливает текущий цвет фона, используя палитру, в данном случае – это светло-синий цвет.

8. Procedure MaxMinF – вычислят максимальные и минимальные значения функции f(x).