Курсовая работа: Метод Ньютона для решения нелинейных уравнений

Вычисления производить с точностью ε = 0, 001.

Решение:

Вычислим первую производную функции.

F’(x)=2x cosx² - 2x sinx² - 10.

Теперь вычислим вторую производную от функции.

F’’(x)=2cosx² - 4x² sinx² - 2sinx² - 4x² cosx² = cosx² (2-4x² ) - sinx² (2+4x² ).

Построим приближённый график данной функции.

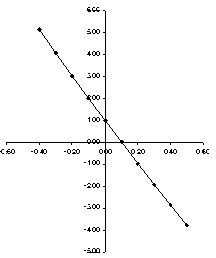
Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x⁽⁰⁾ ) * f’’(x⁽⁰⁾ ) > 0.

Пусть x⁽⁰⁾ = 0, 565, тогда f(0. 565)*f’’(0. 565) = -4. 387 * (-0. 342) = 1. 5 > 0,

Условие выполняется, значит берём x⁽⁰⁾ = 0, 565.

Теперь составим таблицу значений, для решения данного уравнения.

k	x(k)	f(x(k))	f’(x(k))	| x(k+1) - x(k) |
0	0. 565	-4. 387	-9. 982	0. 473
1	0. 092	0. 088	-9. 818	0. 009
2	0. 101	0. 000	-9. 800	0. 000
3	0. 101

Отсюда следует, что корень уравнения х = 0, 101.

Пример 2

Решить уравнение методом Ньютона.

cos x – e^-x2/2 + x - 1 = 0

Вычисления производить с точностью ε = 0, 001.

Решение:

Вычислим первую производную функции.

F’(x) = 1 – sin x + x*e^-x2/2 .

Теперь вычислим вторую производную от функции.

F’’(x) = e^-x2/2 *(1-x² ) – cos x.

Построим приближённый график данной функции.

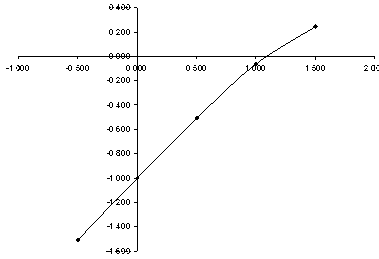
Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x⁽⁰⁾ ) * f’’(x⁽⁰⁾ ) > 0.

Пусть x⁽⁰⁾ = 2, тогда f(2)*f’’(2) = 0. 449 * 0. 010 = 0.05 > 0,

Условие выполняется, значит берём x⁽⁰⁾ = 2.

Теперь составим таблицу значений, для решения данного уравнения.

k	x(k)	f(x(k))	f’(x(k))	| x(k+1) - x(k) |
0	2	0. 449	0. 361	1. 241
1	-0. 265	0. 881	0. 881	0. 301
2	-0. 021	0. 732	0. 732	0. 029
3	0. 000	0. 716	0. 716	0. 000
4	1. 089

Отсюда следует, что корень уравнения х = 1. 089.