Курсовая работа: Модель дослідження стійкості та якості перехідних процесів слідкувальної системи
1) У першому рядку таблиці записують коефіцієнти характеристичного рівняння, що мають парні індекси в порядку їх зростання.
2) У другому рядку таблиці записують коефіцієнти з непарними індексами в порядку їх зростання.
3) У подальші рядки вписують коефіцієнти, визначені як
де – i – індекс, що позначає номер рядка таблиці
– індекс, що позначає номер стовпця таблиці.
4) Число рядків таблиці Рауса на одиницю перевищує порядок характеристичного рівняння замкнутої САУ.
Умови стійкості Рауса: Щоб САУ була стійкою необхідно і достатньо, щоб всі коефіцієнти першого стовпця таблиці Рауса мали один і той же знак, тобто були позитивними. Якщо не всі коефіцієнти першого стовпця таблиці Рауса позитивні, тобто САУ нестійка, число правого коріння характеристичного рівняння рівне числу змін знаку в першому стовпці таблиці Рауса.
Критерій Гурвіца
Цей критерій дозволяє визначити стійкість САУ, якщо характеристичне рівняння замкнутої системи представлене у вигляді:
Для цього будується головний визначник Гурвіца за наступним правилом: по головній діагоналі виписуються всі коефіцієнти від до в порядку зростання коефіцієнтів. Стовпці вгору від головної діагоналі заповнюються коефіцієнтами характеристичного рівняння з послідовно зростаючими індексами, а стовпці вниз – коефіцієнтами з послідовно убиваючими індексами. На місці коефіцієнтів з індексами, великими порядку характеристичного рівняння і меншими нуля, проставляють нулі.
Виділяючи в головному визначнику Гурвіца діагональний мінор, отримуємо визначника Гурвіца нижчого порядку. Номер визначника Гурвіца визначається номером коефіцієнта по діагоналі, до якого складають даного визначника.
, 
, 
.
Умовою даного критерію є, щоб САУ була стійка, необхідно і достатньо, щоб визначник Гурвіца і його діагональний мінор мали знаки, однакові із знаком першого коефіцієнта характеристичного рівняння замкнутої САУ. При для стійкості САУ необхідно і достатнє виконання умов:
;.
Розглянемо замкнуту САУ, що складається з трьох послідовно включених аперіодичних ланок, охоплених 100% зворотним зв'язком.
Передавальна розімкненою САУ функція має вигляд:
.
Передавальна функція замкнутої САУ визначається як
.
Головний визначник Гурвіца має вигляд:
.
Перший визначник Гурвіца 
. Ця умова виконується для всіх
можливих комбінацій параметрів САУ.
Другий визначник Гурвіца визначається як
.
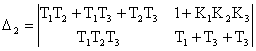Розкриваючи визначника отримуємо