Курсовая работа: Модель распределения
Обычно бывает затруднительно исследовать генеральную совокупность. Тогда проводят исследование выборочной совокупности, и его результаты распространяют на генеральную совокупность.
Наиболее часто для формирования выборочной совокупности применяют бесповторную случайную выборку. Случайный отбор организуют с помощью жребия, таблицы случайных чисел или программы, генерирующей квазислучайную последовательность чисел. Для этого единицы генеральной совокупности нумеруют. Данные, соответствующие выпавшим, номерам попадают в выборку. При этом повторяющиеся номера пропускаем.
Покажем применение таблицы случайных чисел. В табл. 1 приложения приведено пятьсот четырехзначных случайных чисел.
Рассмотрим пример получения выборки. Генеральная совокупность содержит значения восьми количественных экономических показателей для 100 предприятий. Она представлена в табл.2 приложения.
Наиболее проработанной в статистике является парная корреляция. Положим, нужно установить корреляционную связь между двумя показателями. В нашем случае мы изучаем связь между годовой балансовой прибылью (показатель 5) и электровооруженностью на одного работающего (показатель №7), выбираем в табл.1 приложения четырёхзначное число из 7-го столбца, 5-ой строки; т.к. сумма номеров показателей чётна, то из него берём правую половину; далее выбираем 30 неповторяющихся чисел. Затем из табл.2 приложения выбираем в соответствующих номерах строк 30 пар значений изучаемых показателей, в соответствии с этими данными получаем табл.1.1
Таблица 1.1
| № строки | 5 | 7 |
| 5 | 40,2 | 35,6 |
| 12 | 35,4 | 32,9 |
| 13 | 31,4 | 30,5 |
| 18 | 42,8 | 37,7 |
| 22 | 36,6 | 33,7 |
| 26 | 37,8 | 34,3 |
| 27 | 44,5 | 38,4 |
| 30 | 42,7 | 37,2 |
| 31 | 32,8 | 31,3 |
| 32 | 32,5 | 30,7 |
| 36 | 32,7 | 31,4 |
| 38 | 38,9 | 35,3 |
| 40 | 33,2 | 31,6 |
| 41 | 36,2 | 33,7 |
| 43 | 33,3 | 31,4 |
| 45 | 36,2 | 33,5 |
| 46 | 38,4 | 34,6 |
| 49 | 38,8 | 35,1 |
| 52 | 35,7 | 33,2 |
| 54 | 33,7 | 32 |
| 57 | 36,3 | 33,6 |
| 60 | 40,3 | 36,1 |
| 65 | 35,8 | 32,8 |
| 68 | 33,7 | 31,9 |
| 69 | 41,6 | 36,3 |
| 71 | 38,8 | 35 |
| 76 | 34,9 | 32,6 |
| 80 | 39,4 | 35,8 |
| 86 | 37,1 | 33,5 |
| 91 | 35,9 | 32,6 |
| 99 | 4 | 42,2 |
2. Построение интервального ряда распределения
Этот и последующие этапы работы в этом разделе выполняем для каждого изучаемого признака в отдельности.
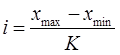 |
???????? ?? ????????, ??? ?????????? ???????????? ???????? n ????????, ???????? ?????? ?????????? ???????? ?? ??????? ?.?. ??????????:
где К = 1+3,322gn- число интервалов; при n=30 К=5. xmax иxmin - минимальное и максимальное значения признака.
Определяем границы интервалов. Для первого интервала левая граница равна xmin, а правая – xmin +i и, для второго, соответственно - xmin +i и xmin +2i и т.д.
Строим таблицу частоты распределения значений признака по интервалам и гистограмму. Для определенности считаем, что значение признака, лежащее на границе двух интервалов, попадает в правый интервал.
Для показателя x: ![]()
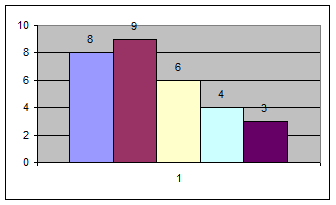
Определяем границы интервалов и строим таблицу частоты распределения значений признака по интервалам:
| Границы интервалов | Число предприятий | |
| 31,4 | 34,02 | 8 |
| 34,02 | 36,64 | 9 |
| 36,64 | 39,26 | 6 |
| 39,26 | 41,88 | 4 |
| 41,88 | 44,5 | 3 |
Строим гистограмму:
Для показателя y: ![]()
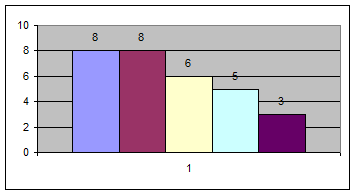
Определяем границы интервалов и строим таблицу частоты распределения значений признака по интервалам:
| Границы интервалов | Число предприятий | |
| 30,5 | 32,08 | 8 |
| 32,08 | 33,66 | 8 |
| 33,66 | 35,24 | 6 |
| 35,24 | 36,82 | 5 |
| 36,82 | 38,4 | 3 |
Строим гистограмму:
3. Проверка соответствия эмпирического распределения нормальному закону распределения
Для проверки соответствия эмпирического распределения случайной величины нормальному закону распределения в нашем случае (при n<30) можно использовать критерии Шапиро-Уилкса (W) и Колмогорова (D). В нашем случае мы используем критерий Колмогорова.
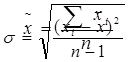 |
??????? ????????? ??????? ????????
 Для признака x:
Для признака x:
 Для признака y:
Для признака y:
Вычисляем ошибку определения средней по выборочной совокупности (ошибку выборки):
 |
??? n - ??????????? ???????; N= 100 - ??????????? ??????????? ????????????; t - ??????????? ???????; ??? ????????????? ??????????? 95,45% t=2.
Для признака x:
Для признака y:
Генеральная средняя располагается в следующих границах:
![]()
Определяем эти границы:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--