Курсовая работа: Модель распределения
Обычно для расчётов используют ежемесячные данные за один год или несколько лет. В этом случае интервал между двумя соседними месяцами принимают равным:
![]()
Построив модель сезонных колебаний, положим для уточнённого изучения основной тенденции a0 =0. Исключим сезонные колебания из уровней динамического ряда (табл.3.1.1).
Таблица 3.1.1
| xt | yt |
| 2661,669 | 3613,236 |
| 2875,587 | 3822,011 |
| 2963,355 | 3982,202 |
| 3123,42 | 4283,029 |
| 3220,836 | 4428,087 |
| 3326,98 | 4610,676 |
| 3286,852 | 4566,172 |
| 3263,324 | 4538,486 |
| 3116,237 | 4319,251 |
| 3036,962 | 4198,99 |
| 2900,234 | 3993,958 |
| 2894,491 | 3990,848 |
| 2874,626 | 3974,423 |
| 2997,766 | 4181,021 |
| 3084,173 | 4339,299 |
| 3262,659 | 4638,991 |
| 3338,698 | 4783,995 |
| 3444,038 | 4907,625 |
| 3403,894 | 4924,979 |
| 3381,141 | 4899,469 |
| 3315,414 | 4682,148 |
| 3157,719 | 4563,026 |
| 3022,368 | 4358,052 |
| 3017,432 | 4353,904 |
| 2997,586 | 4365,623 |
2. Определение основной тенденции развития
Для выявления основной тенденции развития применяют аналитическое выравнивание. В результате выравнивания получают зависимость изучаемого показателя от времени, т.е. трендовую модель. Используем линейную трендовую модель:
Наиболее тщательно выбирают модель для целей экстраполяции значений показателя. Значение х и у выбираем из табл.6 приложения.
Коэффициенты уравнения определяем методом наименьших квадратов. В нашем случае система уравнений относительно коэффициентов a0 и a1 имеет вид:
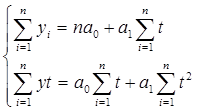 |
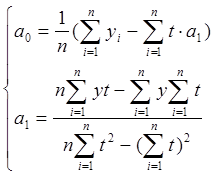 и коэффициенты a0 и a1 равны:
и коэффициенты a0 и a1 равны:
Для признака x:
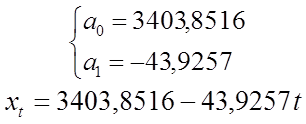 |
Для признака y:
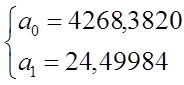
3. Изучение корреляционной зависимости между уровнями двух динамических рядов
Продолжаем рассмотрение двух выбранных нами рядов динамики. При исследовании тесноты связи между их уровнями на первое место выступает анализ смысла связи между рядами и установление факторного и результативного признаков. Без такого анализа значение коэффициента корреляции может выражать только случайное сопутствие в изменении уровней двух рядов.
Применение традиционных приемов изучения корреляции к динамическим рядам сопряжено со следующими особенностями:
1. В социально-экономических рядах динамики имеет место тенденция, вызванная действием постоянных факторов: последующие уровни рядов динамики зависят от последующих, т.е. имеется автокорреляция и авторегрессия. Это говорит о том, что нарушена одна из предпосылок применения теории корреляции - независимость отдельных наблюдений друг от друга. Если автокорреляцией при этом пренебречь, то полученная зависимость будет отражать взаимосвязь, которой в действительности не существует, или искажать реально существующую взаимосвязь.
2. Второй особенностью изучения корреляции динамических рядов является наличие временного лага, т.е. сдвига по времени изменения уровней одного ряда по отношению к изменению уровней другого ряда. Если сдвинуть уровни одного ряда относительно другого и убрать временной лаг, то получим верную оценку тесноты корреляционной связи уровней двух динамических рядов.
3. Третьей особенностью является изменение тесноты корреляционной связи уровней динамических рядов со временем.
Вначале устраняем временной лаг, значение которого определяем графически или подбором; с расчетом коэффициента корреляции.
Затем приступаем к исследованию взаимосвязи уровней. Существует четыре направления изучения корреляционной зависимости между уровнями двух динамических рядов:
- коррелирование уровней;
- коррелированно разностей;
- коррелирование остатков (отклонений от трендов);
- коррелирование с учетом фактора времени.
3.1. Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования уровней
Нам следует построить уравнение авторегрессии для каждого из изучаемых динамических рядов, проверив наличие временного лага:
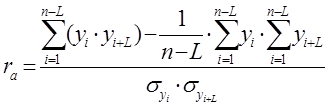 |
где L – величина временного лага (L=1).
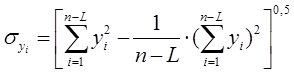 | |
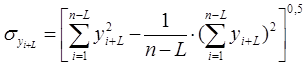 |
Для динамического ряда xi :
![]() Для динамического ряда yi :
Для динамического ряда yi :
Т.к. полученные коэффициенты корреляции больше табличного, то переходим к следующему методу.
3.2. Изучение корреляционной зависимости между уровнями двух динамических рядов методом коррелирования разностей
По первоначальным динамическим рядам xi , yi с количеством членов n строим новые динамические ряды ui , wi с количеством членов n-1(табл.3.2.1), где:
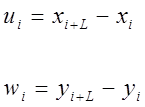 |
Таблица 3.2.1
| ui | wi |
| 640 | 224 |
| 336 | -164 |
| 164 | -276 |
| -144 | -530 |
| -316 | -410 |
| -530 | -396 |
| -450 | -44 |
| -396 | 104 |
| -84 | 456 |
| 104 | 470 |
| 416 | 590 |
| 470 | 336 |
| 550 | 224 |
| 336 | -164 |
| 184 | -276 |
| -164 | -530 |
| -316 | -470 |
| -530 | -336 |
| -450 | -44 |
| -316 | 104 |
| -164 | 456 |
| 104 | 470 |
| 416 | 590 |
| 470 | 366 |