Курсовая работа: Модель распределения

Решая первое уравнение относительно а, получим:

Т.о.:

???????? ??????????? ?????????? ?????:

где s_x и s_y - средние квадратические отклонения признаков x и y.

?????????? ????? ?????????:

и остаточную дисперсию:

где y_x (х_i ) - значение величины y, рассчитанное по уравнению регрессии при подстановке в него значения x_i ; y_i - значение величины y в исходной таблице, соответствующее значению x_{i .}

Определим индекс корреляции:

Индекс корреляции принимает значения 0£ i £1.

Т.к. i близок к единице, то связь между признаками хорошо описана выбранным уравнением регрессии. Для линейной зависимости дополнительным условием для такого заключения является близость значений r и i.

????? ??????? ????????? ????? ????????? ?????????. ????????? ?? ??? ????? ?? ?????????, ???????? ????????????? ??????? ??????? ?????????????? ?????? ????????? ?????????:

где m - число коэффициентов в уравнении регрессии.

Принимая во внимание то, что мы имеем дело с малой выборкой, необходимо оценить значимость коэффициентов уравнения регрессии, а также индекса корреляции i и линейного коэффициента корреляции r. Значимость линейного коэффициента корреляции r оцениваем с помощью критерия Стьюдента. Фактическое значение критерия Стьюдента равно:

Критическое (предельное) значение критерия Стьюдента t_k , берем из табл.4 приложения, задаваясь уровнем значимости a=5,0 и имея число степеней свободы равное:

k=n-2

Если t_r >t_k , то величину линейного коэффициента корреляции считаем значимой и можем использовать в расчетах.

?????????? ????????????? ????????? ????????? ? ? b ????? ????????? ? ??????? ???????? ?????????. ????????? ???????? ???????? ????????? ?????:

Учитывая, что число степеней свободы также равно k=n-2, сравнение фактических значений критерия Стьюдента ведем с уже найденным критическим значением t_k .

Если t_a >t_k , t_b >t_k , то соответствующий коэффициент уравнения регрессии значим, и мы можем им пользоваться. Значимость индекса корреляции определяем с помощью критерия Фишера. Фактическое значение критерия Фишера равно:

??? m - ????? ????????????? ? ????????? ?????????.

Табличное значение критерия Фишера F_k ; определяется по табл.5 приложения, задаваясь уравнением значимости a и числом степеней свободы k₁ =m-l; k₂ =n-m.

Если Fi>Fk, то величину индекса корреляции считаем значимой и можем ее использовать в расчетах.

Если коэффициенты а и b, а также линейный коэффициент корреляции r и индекс корреляции i значимы, то все наши расчеты и выводы, опирающиеся на эти величины, правомерны и мы можем использовать полученное уравнение регрессии для прогноза. Ошибка прогноза будет зависеть, в частности, от остаточной дисперсии s² _e .

Раздел 3. Изучение динамических рядов

1. Изучение сезонных явлений

Исследуем сезонные процессы в наших двух динамических рядах. При изучении сезонных явлений из уровней динамического ряда целесообразно вычесть значения, получаемые по уравнению тренда, которые отражают основную тенденцию развития.

При изучении периодических процессов в качестве аналитической модели используем ряд Фурье:

где k=1; j=1.

Для нахождения коэффициентов a₀ , a_j , b_j применяем метод наименьших квадратов.

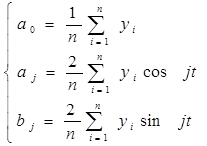Получаем: