Курсовая работа: Модели и методы принятия решений
· Решить задачу средствами MSExcel.
· Решениепроиллюстрировать графически.
maxj (X) = 2x1 + 4x2 – x12 – 2x22
при x1 + 2x2 £ 8
2x1 – x2 £ 12
X³ 0
Задача 1
Решить графоаналитическим методом.
minj (X) = – 3x1 – 2x2
при 2x1 + x2 ³ 2
x1 + x2 £ 3
– x1 + x2 ³ 1
X³ 0
Решение:
Построим линии ограничений:
Примем: 2х1+х2=2 (a)
х1+х2=3 (b)
-х1+х2=1 (c)
экстремум функция минимизация алгоритм
Получаем три прямые a, b и c, которые пересекаются и образуют треугольник соответствующий области которая соответствует первым трем ограничениям, добавляя четвертое ограничение получаем четырехугольник ABCD – допустимая область значений, в которой надо искать минимум (на рисунке эта область не заштрихована).
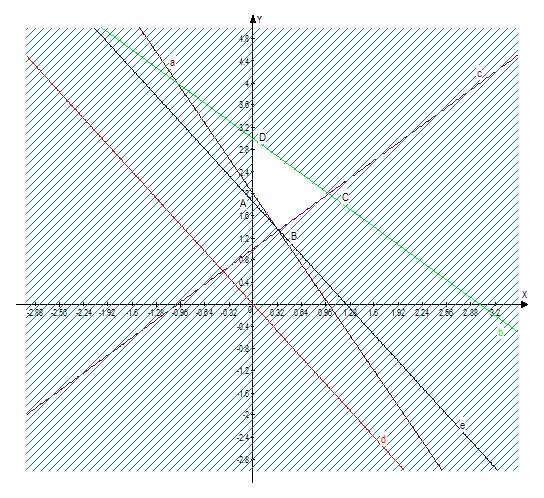
Рис. 1
Примем целевую функцию равной нулю (красная линия d) тогда градиент имеет координаты (-3;-2). Для того, чтобы найти минимум целевой функции будем перемещать график линии d параллельно самой себе в направлении антиградиента до входа ее в область ограничений. Точка в которой область войдет в допустимую область и будет искомой точкой минимума целевой функции. Это точка В(0,33 ; 1,33). При этом целевая функция будет иметь значение:
![]()
Темно-синяя линия на рисунке (е).
Задача 2.
· Найти экстремумы методом множителей Лагранжа.
· Решение проиллюстрировать графически.
extrj (X) = x12 + x22