Курсовая работа: Моделирование рассеяния плоской упругой продольной волны на упругом однородном изотропном цилиндрическом слое

,

получающемуся при подстановке (1.8) в (1.4). Продольная и поперечная части монохроматической волны удовлетворяют уравнениям Гельмгольца:

, (1.9)

где 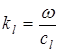, 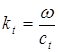- волновые векторы продольной и поперечной волн.

Пусть , а , где - скалярная функция, - векторная функция (соответственно скалярный и векторный потенциалы смещений, или продольный и поперечный потенциалы).

Покажем, что функции и удовлетворяют уравнениям Гельмгольца. Для этого подставим в уравнение движения упругой среды (1.4) вектор , и, изменяя порядок дифференцирования, получим:

Видно, что уравнение будет удовлетворяться, если положить:

,

Если мы будем рассматривать зависимость от времени t у функций и как , то мы получаем уравнения Гельмгольца:

Произвольную плоскую волну можно разложить в спектр, то есть можно ее представить в виде суперпозиции плоских же гармонических волн. Поэтому имеет смысл изучать распространение гармонических волн. Зависимость от координат x,y в декартовой системе координат и времени t мы будем брать в виде экспоненты. Этот же результат можно получить, если применить к уравнениям Гельмгольца для потенциалов, записанным в декартовой системе координат, метод разделения переменных.

1.2 Граничные условия

Рассмотрим граничные условия на границе раздела сред при распространении упругой волны. Они заключаются в непрерывности компонент вектора смещения и непрерывности нормального и касательных , компонент тензора напряжений при переходе через границу раздела сред.

В изотропной среде компоненты тензора напряжений связаны с компонентами тензора деформаций при помощи закона Гука (1.6), а компоненты тензора деформаций связаны с компонентами вектора смещений с помощью формулы (1.3). Рассмотрим цилиндрическую границу в цилиндрической системе координат. Если систему прямоугольных координат выбрать таким образом, что ось z является осью цилиндра, то компоненты тензора напряжений выразятся через компоненты вектора смещения по формулам:

, (1.10)

где - нормальная компонента тензора напряжений, - касательные компоненты, и - упругие константы Ламе.

2. РАССЕЯНИЕ ПЛОСКОЙ ПРОДОЛЬНОЙ УПРУГОЙ ВОЛНЫ ОДНОРОДНЫМ ИЗОТРОПНЫМ ЦИЛИНДРИЧЕСКИМ СЛОЕМ

2.1 Постановка задачи

Рассмотрим бесконечный изотропный полый круговой цилиндр с внешним радиусом и внутренним - , модули упругости и плотность материала которого . Цилиндрическая система координат выбрана таким образом, что координатная ось z является осью вращения цилиндра. Будем считать, что окружающее и находящееся в полости упругие среды являются изотропными и однородными, имеющими плотности и модули упругости , соответственно.

Пусть из полупространства на упругий цилиндрический слой параллельно оси Ох в плоскости Оxy падает плоская упругая монохроматическая волна:

Определим отраженную от слоя и прошедшую через слой волны, а также найдем поле смещений внутри упругого слоя.

Фронт падающей волны перпендикулярен образующим цилиндра и поэтому задача является плоской, то есть смещения не зависят от координаты z.

Учтем, что в формуле , представляющей собой общее выражение для смещения, потенциал в силу выбранной системы координат мы выбрали так, чтобы единственной отличной от нуля была компонента . Поэтому в силу линейности задачи мы можем рассматривать отдельно падение продольной волны , сдвиговой волны , где .

Мы осстановимся на рассмотрении рассеяния плоской продольной волны, представленной вектором падения: .

2.2 Рассеяние продольной волны

Пусть из внешнего пространства на упругий цилиндр перпендикулярно падает плоская упругая продольная волна, потенциал смещений которой равен: