Курсовая работа: Мономиальные динамические системы

Тогда .

Определение 1.2.2.

Обозначим для .

Видно что – линейное преобразование - элемента. Но можно рассматривать его, как линейное преобразование для - элемента, рассматривая как конечное кольцо, которое обозначим – . То есть, имеется линейное преобразование .

Это доказывает следующую лемму.

Лемма 1.2.2.

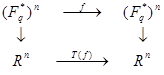- коммутативная диаграмма.

Обратим внимание, что вертикальные стрелки – изоморфизмы. Это значит, что они сохраняют фазовое пространство структуры, включая длину конечных циклов. В частности, имеется следующее следствие.

Следствие 1.2.3.

Фазовое пространство изоморфно к подграфу фазового пространства , состоя из всех наборов с базисным вектором .

Пример 1.2.2.

Для мономиальной системы в примере 1.2.1, определим , где

.

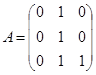Рассчитаем переходы в фазовом пространстве .

000 - ,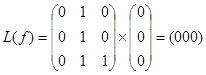

001 - ,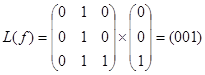

010 - ,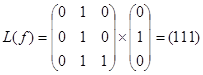

011 - ,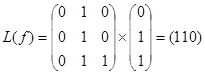

100 - ,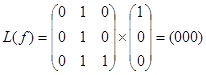

101 - ,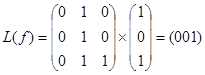

110 - ,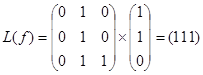

111 - .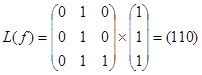

Фазовое пространство изображено на рисунке 1.2.3.

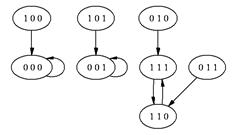
Рис. 1.2.3. Фазовое пространство .

Теорема 1.2.1.

Пусть – мономиальная динамическая система. Тогда – система конечных элементов тогда, и только тогда, когда и – системы конечных элементов.

Доказательство.

Из следствий 1.2.1 и 1.2.3, если – система конечных элементов, то и тоже системы конечных элементов. Для доказательства от противного, предположим что и – системы конечных элементов, а – нет. Для каждого конечного цикла , любой из двух связанных наборов имеет все координаты ненулевые, или все наборы имеют минимум одну нулевую координату. В первом случае из этого следует, что имеет конечный цикл, той же длины. Следовательно, если имеет конечный цикл длины большей чем , тогда включаются только наборы имеющие минимум одну нулевую координату.