Курсовая работа: Некоторые приложения определенного интеграла в математике

Другим видом несобственного интеграла является интеграл , если функция f не ограничена на , но непрерывна на при любом , (или на ), т.е. не ограничена в окрестности точки (точки b).

Этот интеграл существует (сходится), если существует:

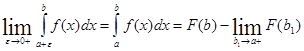
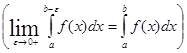
Пример.

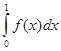, если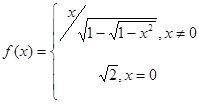

f(x) непрерывна на [0,1]. После замены получаем

.

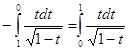не ограничена на [0,1], т.к. первообразная функция на при любом , равна: , то

.

Несобственный интеграл может появится и при интегрировании по частям.

,

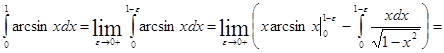
т.е.

,

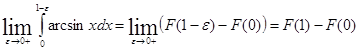где - первообразная для arcsinx на [0,1].

4.1.Формула Валлиса.

Для вывода формулы Валлиса необходимо вычислить следующий интеграл:

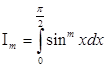(при натуральном m).

Интегрируя по частям, найдём

.

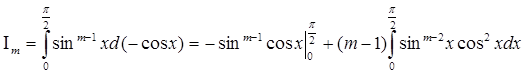Двойная подстановка обращает в нуль. Заменяя через , получим

откуда рекуррентная формула:

,