Курсовая работа: Некоторые приложения определенного интеграла в математике

,

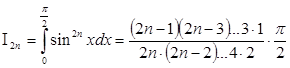если же m=2n+1, то

.

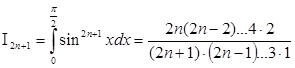Такие же точно результаты получаются и для .

Для более короткой записи найденных выражений воспользуемся символом m!!(произведение натуральных чисел, не превосходящих m и одной с ним чётности). Тогда можно будет написать

при m нечетном нечётном.

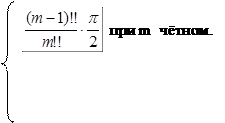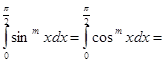(1)

Из формулы (1) можно вывести знаменитую формулу Валлиса (J. Wallis).

Предполагая 0<x<, имеем неравенства

.

Проинтегрируем эти неравенства в промежутке от 0 до :

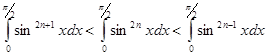
Отсюда, в силу (1), находим

или

.

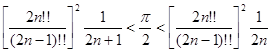Так как разность между двумя крайними выражениями

,

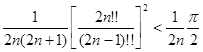очевидно, стремится к 0 при , то является их общим пределом. Итак,

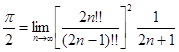
или

.

Отсюда в свою очередь вытекает

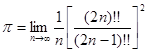
Эта формула носит название формулы Валлиса. Она дает довольно простое выражение числа p через натуральные числа. Теоретически этот результат интересен. Что касается ценности этой формулы как средства фактического вычисления p, то она невелика. Именно, чтобы получить удовлетворительную точность, надо взять n довольно большим, а тогда выражение оказывается весьма громоздким.

4.2. Применение формулы Валлиса для интеграла Эйлера-Пуассона.

Интеграл Эйлера-Пуассона имеет вид:

;

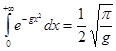Приведём метод его нахождения. Мы знаем что положив:

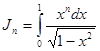(т.к. ),