Курсовая работа: Некоторые замечательные кривые

Лемниската есть частный вид линии Кассини. Однако, хотя линии Кассини получили всеобщую известность с 1749 г., тождественность «восьмерки Кассини» с лемнискатой Бернули была уставновлена лишь в 1806 г. (итальянским математиком Саладини ).

5.3 Построение

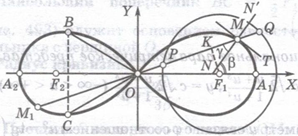
Можно применять общий способ построя линия Кассини, но нижеизложенный способ (К. Маклорена ) и проще и лучше. Строим (см. рис.) окружность радиуса с центром в точке F₁ (или F₂ ). Проводим произвольную секущую OPQ и откладываем на этой прямой в обе стороны от точки O отрезки OM и OM₁ , равные хорде PQ. Точка M опишет одну из петель лемнискаты, точка M₁ – другую.

5.4 Особенности формы

Лемниската имеет две оси симметрии: прямую F₁ F₂ (OX) и прямую OYOX. Точка O – узловая; обе ветви имеют здесь перегиб. Касательные в этой точке составляют с осью OX углы . Точки A₁ ,A₂ лемнискаты, наиболее удаленные от узла O (вершины лемнискаты), лежат на оси F₁ F₂ на расстоянии от узла.

5.5 Свойства нормали.

Подяоный радиус OM лемнискаты образует с нормалью MN угол , вдвое больше полярного угла :

.

Другими словами: угол между осью OX и вектором NN^' внешней нормали лемнискаты в точке M равен утроенному полярному углу точки M:

.

5.6 Построение касательной

Чтобы построить касательную к лемнискате в ее точке M, проводим полярный радиус OM и строим . Перпендикуляр MT к прямой MN есть искомая касательная.

5.7 Задача

Написать уравнение лемнискаты Бернулли в прямоугольной системе координат (O – серидина отрезка F₁ F₂ ) и в полярной системе координат (O – полюс).

Решение:

Пусть точка O – начало координат ; ось OX направлена по F₁ F₂ . Тогда Уравнение в прямоугольной системе координат:

.

Если O – полюс, OX – полярная ось, то уравнение в полярной системе:

.

Угол изменяется в промежутках и .

Заключение

В данной работе мы рассмотрели некоторые замечательные кривые, изучили их способы построения, особенности формы и задачи, связанные с этими кривыми.

В параграфе 1 была рассмотрена строфоида, особенности её формы, стереометрическое образование и исторические сведения.

Во 2-м параграфе мы изучили циссоиду Диокла и некоторые формулы, связанные с ней.

В параграфе 3 узнали метод построения, особенности формы и исторические сведения о кривой, называемой «Декартов лист».

В 4-м параграфе рассмотрели улитку Паскаля. Её определение, построение, особенности формы, свойства нормали и построение касательной.

В параграфе 5 была изучена лемниската Бернулли: определение, построение, исторические сведения, особенности формы, свойства нормали и построение касательной.

А также при помощи задач узнали формулы кривых в прямоугольной декартовой и полярной системах координат.