Рисунок 2.3 Спектры сигналов ЧМ при различных индексах модуляции М

3. Расчет вероятности ошибки на выходе приемника

Вычислим мощность шума на выходе приемника по формуле:

, где

полоса пропускания приемника для ДЧМ;

где T – длительность сигнала;

Отношение мощности сигнала к мощности шума (h² ):

; ,

где P_С – мощность приходящего сигнала;

Для расчёта вероятности ошибки на выходе приёмника воспользуемся формулой:

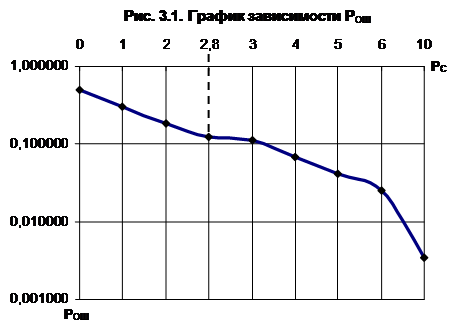
Построим зависимость вероятности ошибки от отношения мощности сигнала к мощности шума (h). Результаты расчетов сведены в таблицу 3.1 График зависимости Р_ош от h² , изображен на рисунке 3.1

Таблица №3.1

РС мВт	0	1	2	2,8	3	4	5	6	10
h2	0	1	2	2,8	3	4	5	6	10
h	0	1	1,414	1,67	1,732	2	2,236	2,449	3,1623
РОШ	0,500000	0,303265	0,183940	0,123298	0,111565	0,067668	0,041042	0,024894	0,003369

4. Сравнение выбранной схемы приемника с оптимальным приемником

Решая вопрос о помехоустойчивости системы связи следует вначале остановиться на выборе критерия помехоустойчивости . Таких приборов может быть предложено достаточно много: минимума вероятности ошибочного приёма, минимума среднего риска или среднеквадратичного отклонения от передаваемого сообщения и т.д. Эта задача усложняется, если рассматривать возможность безошибочного распознавания множества символов. Поэтому рассмотрим наиболее простой (но и наиболее общий для любого числа символов) случай распознавания бинарных сигналов, а для оценки качества – предложенный В.А. Котельниковым, критерий идеального наблюдателя, который обеспечивает минимум вероятности ошибочного приёма.

Если имеются два сигнала S₀ и S₁ поражённых аддитивной помехой n(t), то напряжение на выход приёмника Z(t) = S(t) + n(t), где S(t) может принимать два значения.

Графически области условной вероятности событий S₀ и S₁ будут иметь вид:

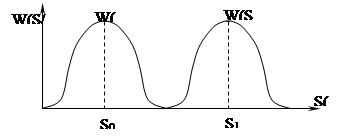Рисунок 4.1. – Условная вероятность.

где W(S₀ /Z) и W(S₁ /Z)- условные плотности вероятности появления сигналов “0” и “1” соответственно, при наличии смеси: сигнал + шум.

S₀ и S₁ – соответственно ожидаемые (или точно известные) значения сигнала “1” и “0”.

Вероятность события P(S) = ∫ W(S/Z)dt. Тогда для нормального закона распределения плотности условных вероятностей событий будем иметь:

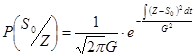
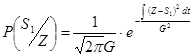
где G – среднеквадратичное значение уровня шума. Найдём совместное решение этих уравнений в виде отношений правдоподобия:

взяв натуральные логарифмы от числителя и знаменателя:

Это выражение – наиболее классический алгоритм решения задачи оптимального приёма, соответствующая ему функциональная схема носит название идеального приёмника Котельникова.