Курсовая работа: Определение основных характеристик цифровой системы передачи сообщ

На рисунке 4.2. обозначены:

НЕ – инвертор (вычитающее устройство)

КВ – квадратор

∫ – интегратор

РУ – решающее устройство

т.о. оптимальный приёмник для разделения бинарных сигналов состоит из двух одинаковых ветвей, на которые заводятся ожидаемые (или известные) значения уровней сигналов “0” и “1” и решающее устройство перебрасывается в сторону большего значения среднего уровня мощности в той или иной ветви.

Но решение задачи возможно и другими способами:

Пологая (минимум ошибки) и раскрывая скобки в подынтегральных выражениях (смотри формулу выше) получим:

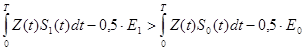
где Е₁ = S₁ ² – энергия сигнала “1”

Е₀ = S₀ ² – энергия сигнала “0”

В этом выражении решение оптимального приёма осуществляется за счёт перемножения смеси входного сигнала на известную функцию S₀ (t) и S₁ (t) с последующим накоплением (интегрированием). Такой способ приёма (по виду математической обработки) носит название корреляционного. Соответствующая сема на рисунке 4.3.

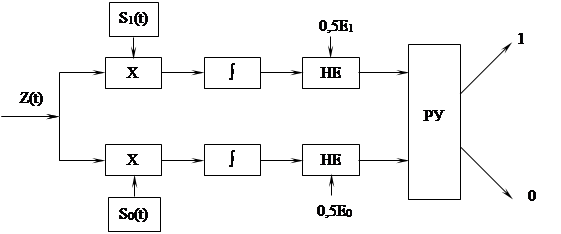Рисунок 4.3.

Выражение представленное выше может быть ещё более упрощено, если ввести понятие разности сигналов S_∆ (t) = S₁ – S₀ тогда

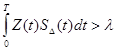
где - пороговый уровень различения.

Тогда функциональная схема одноканального оптимального приёмника бинарных сигналов будет иметь вид Рисунок 4.4.

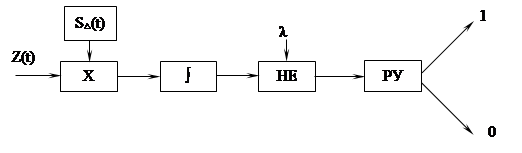Рисунок 4.4.

Решение задачи в пользу сигнала 1 будет в том случае, если сигнал на выходе интегратора > λ.

Обратим внимание, что функция корреляции смеси сигнала с полезной информацией может быть получена, когда в точке приёма точно известен принимаемый сигнал. Если последнее условие трудно осуществить, то можно осуществить необходимую значимость путём приёма исходного сигнала Z(t) на согласованный фильтр, переходная характеристика которого

.

Таким образом, схема рисунок 4.4. для не полностью известного сигнала в точке приёма будет рисунок 4.5.

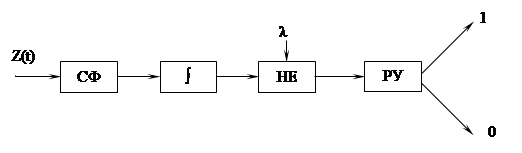Рисунок 4.5.

Следует отметить, что задачей согласованного фильтра является не восстановление формы сигнала искаженной шумом, а получение одного отсчета, по которому можно было бы судить о присутствии или отсутствии на входе фильтра сигнала известной формы.

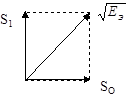
Сигналы «0» и «1» равны по амплитуде, но отличаются по частоте, при этом спектральные линии полезной информации различаются на p/2 (выполняется условие ортогональности) - S₁ и S_O комплексно сопряжены.

S₁ (t)=Acos w ₁ t; S₀ (t)= Acos w ₀ t; 0 < t < Т

Так как сигналы S₁ и S₂ взаимоортогональны, то их функция взаимокорреляции

B_{S 1 S 0} (0) = 0E₁ =Е₀ E_Э =2Е₁