Курсовая работа: Определение основных характеристик цифровой системы передачи сообщ

(6.2)

На практике применяется как блочное, так и непрерывное кодирование. При блочном кодировании последовательный цифровой код символов разбивается на блоки по k символов в каждом. Затем каждому такому k–значному блоку сопоставляется n–значный блок, в котором k кодовых символов называется информационными, а r=(n-k) – корректирующими. Простейшим вариантом такого кода является код с проверкой на четность. Если число единиц в информационном блоке четное, то добавляется 0, если нечетное, то –1.

Вероятность ошибки, необнаруженной этим кодом при независимых ошибках, определяется биноминальным законом:

(6.3)

где р – вероятность искажения одного элемента кода.

В нашем случае число информационных элементов k=7, код с параметрами (n,k) = (8,7) и по формуле (6.3) имеем:

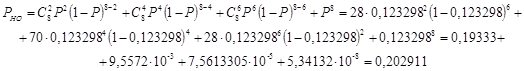
Избыточностью равномерного кода называют величину

(6.4)

для нашего кода

7. Статистическое кодирование

Цели помехоустойчивого и статистического кодирования различны. При помехоустойчивом кодировании увеличивается избыточность за счет введения дополнительных элементов в кодовые комбинации. При статистическом кодировании, наоборот, уменьшается избыточность, благодаря чему повышается производительность источника сообщений.

Количественной мерой информации является логарифмическая функция вероятности сообщения:

(7.1)

Основание логарифма чаще всего берется 2. При этом единица информации называется двоичной единицей или бит. Она равна количеству информации в сообщении, происходящем с вероятностью 0,5, т.е. таком, которое может с равной вероятностью произойти или не произойти.

В теории информации чаще всего необходимо знать не количество информации , содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.

Если имеется ансамбль (полная группа) из k сообщений с вероятностямито среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений Н(х), определяется формулой

(7.2)

(7.3)

Размерность энтропии - количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения. Неопределённость максимальна при равенстве вероятностей выбора каждого сообщения:

В этом случае

(7.4)

Вычислим энтропию данного источника:

Чтобы судить насколько близка энтропия источника к максимальной вводят понятие избыточности источника сообщений

(7.5)