Курсовая работа: Определение спектра амплитудно-модулированного колебания
uΩ (t)= 
при 
, (1)
при 
.
Частота синусоиды 
(в знаменателе записан период этой синусоиды).
Значения k1 и b1 определяем из системы уравнений
;
,
получаемой путем подстановки во второе уравнение системы (1) значений времени t1 и 
и соответствующих им значений колебания uΩ (t) (uΩ (t1 )=0, uΩ (t)=-U2 ). Решение указанной системы уравнений дает 
, 
. Аналогично определяем k2 и b2 . В третье уравнение системы (1) подставляем значения t2 и T и соответствующие им значения колебания uΩ (t) (uΩ (t2 )=-U2 , uΩ (T)=0).
;
.
Решив систему, получаем 
, 
В результате изложенного система уравнений (1) принимает вид
при 
,
uΩ (t)= 
при , (2)
при 
.
Для дальнейших расчетов определим:
мкс;
рад/с
рад/с
Для разложения сигнала в ряд Фурье вычислим значения аn , bn , Аn и φn первых пяти гармоник.
4. Определение коэффициентов an
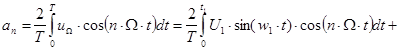
Посчитаем каждый из интегралов отдельно:
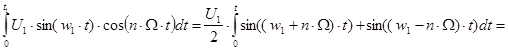
