Курсовая работа: Определение термодинамических активностей компонентов бронзы БрБ2

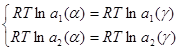(2.7)

Обозначим через х мольные доли компонентов в α-фазе, а через N – мольные доли компонентов в γ-фазе, и учитывая условия нормировки их на единицу, можно систему уравнений (2.7) с учётом (1.3) и (1.6) переписать в следующем виде:

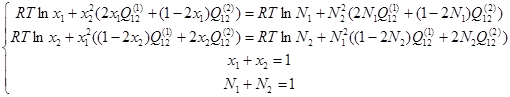(2.8)

Если бы были известны мольные доли x и N при 25°С, то можно было бы с помощью (2.8) непосредственно вычислить значения Q при этой температуре. Однако при столь низкой температуре невозможно получить экспериментальных данных о координатах купола расслаивания. Дело в том, что наступление равновесия между фазами происходит, благодаря диффузии атомов, а в комнатных условиях она протекала бы экстремально долго (несколько сотен лет). Поэтому необходимо изучить температурную зависимость энергий смешения и экстраполировать её на уровень комнатных температур.

Если T=const и известны все x и N, то система уравнений (2.8) линейна относительна параметров Q и может быть решена аналитически.

Обозначим . Если теперь перенести правую часть системы (2.8) в левую, то она перепишется в виде:

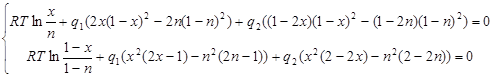(2.9)

Выразим из первого уравнения системы (2.9):

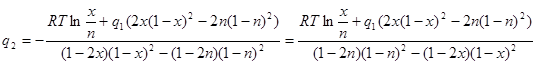(2.10)

Подставим (2.10) во второе уравнение системы (2.9):

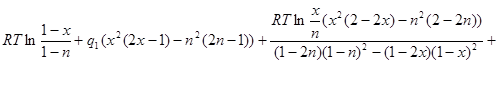
(2.11)

Теперь можно выразить в явном виде величину :

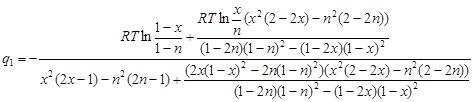(2.12)

Теперь приведём выражения в числителе и знаменателе дроби (2.12) к общему знаменателю:

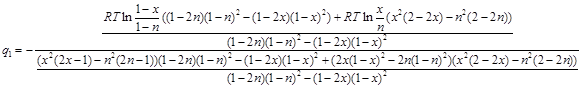
(2.13)

Умножив числитель и знаменатель дроби (2.13) на выражение , окончательно получим:

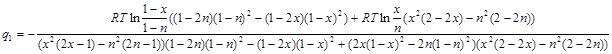
(2.14)

Система уравнений (2.9) не имеет степеней свободы, поэтому случайная погрешность отсутствует. Возможно, пользуясь законом накопления ошибок, определить систематическую погрешность и рассчитать доверительный интервал для значений Q. В данной работе это не учитывается.

Координаты купола расслаивания при различных температурах были сняты с диаграммы состояния Cu – Ni (рис. 1.7) и представлены в таблице 2.1.

Табл. 2.1. Координаты купола расслаивания твёрдого раствора при разных температурах.

t, o C	Состав α-фазы (Cu)		Состав γ-фазы (Ni)
	x1	x2	N1	N2
200	0,650	0,350	0,013	0,987
225	0,633	0,367	0,027	0,973
250	0,580	0,420	0,053	0,947
275	0,513	0,487	0,073	0,927
300	0,467	0,533	0,113	0,887
325	0,387	0,613	0,187	0,813
342	0,300	0,700	0,300	0,700

Для каждой из температур были проведены вычисления значений энергий смешения. вычислены по формуле (2.14), ?