Курсовая работа: Определение законов распределения и числовых характеристик случайной величины на основе опытных данных

Таблица значений границ интервалов и соответствующих частостей , где i= 1, 2, 3, …, k, называется статистическим рядом. Графическим изображением статистического ряда называется гистограмма. Она строится следующим образом: по оси абсцисс откладывают интервалы и на каждом таком интервале, как на основании, строится прямоугольник, площадь которого равна соответствующей частости.

, - высота прямоугольника, .

Таблица

Номер интервала	Левая граница интервала	Правая граница интервала	Интервал	Середина интервала	Частота интервала	Частость интервала	Высота прямо-угольника
1	-8,66	-7,352	(-8,66; -7,352)	-8,006	4	0,04	0,0306
2	-7,352	-6,044	(-7,352; -6,044)	-6,698	3	0,03	0,0229
3	-6,044	-4,736	(-6,044; -4,736)	-5,39	4	0,04	0,0306
4	-4,736	-3,428	(-4,736; -3,428)	-4,082	20	0,2	0,1529
5	-3,428	-2,12	(-3,428; -2,12)	-2,774	26	0,26	0,1988
6	-2,12	-0,812	(-2,12; -0,812)	-1,466	18	0,18	0,1376
7	-0,812	0,496	(-0,812; 0,496)	-0,158	14	0,14	0,1070
8	0,496	1,804	(0,496; 1,804)	1,15	9	0,09	0,0688
9	1,804	3,112	(1,804; 3,112)	2,458	1	0,01	0,0076
10	3,112	4,42	(3,112; 4,42)	3,766	1	0,01	0,0076
Сумма	100	1

Рисунок 1.

Статистическая функция распределения

Статистической функцией распределения называется частость случайной величины, не превосходящая заданного значения Х:

Для дискретной случайной величины Х статистическая функция распределения находится по формуле:

Запишем статистическую функцию распределения в развернутом виде:

где - это середина интервала i, а - это соответствующие частости, где i=1, 2,…, k.

График статистической функции распределения есть ступенчатая линия, точками разрыва которой являются середины интервалов, а конечные скачки равны соответствующим частотам (Рисунок 2).

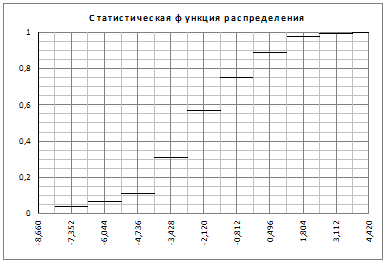
Рисунок 2

Вычисление числовых характеристик статистического ряда

- статистическое математическое ожидание,

- статистическая дисперсия,

- статистическое среднеквадратическое отклонение.

Статистическим математическим ожиданием или статистическим средним называется среднеарифметическое наблюдаемых значений случайной величины Х.

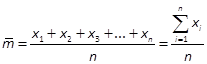
Статистической дисперсией называется среднеарифметическое значение величиныили

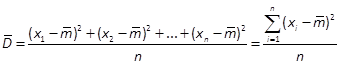
При большом объеме выборки вычисления по формулам и приводят к громоздким выкладкам. Для упрощения расчетов используют статистический ряд с границами и частостями , где i= 1, 2, 3, …, k, находят середины интервалов , а затем все элементы выборки, которые попали в интервал, заменяют единственным значением, тогда таких значений будетв каждом интервале .

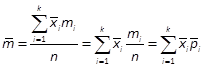
где- среднее значение соответствующего интервала;- частость интервала
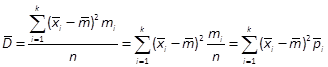