Курсовая работа: Определение законов распределения и числовых характеристик случайной величины на основе опытных данных

Найдем доверительный интервал , в котором находится математическое ожидание. При α = 0.99, n= 100, ,.

по таблицам Лапласа находим:

Отсюда ε = 0,5986.

- доверительный интервал, в котором с вероятностью 99% находится точное значение математического ожидания.

Понятия о критериях согласия

Во многих случаях закон распределения случайной величины неизвестен, но на основании опытных данных делается предположение о виде закона распределения случайной величины Х. Однако для окончательного решения вопроса о виде распределения следует проверить согласуются ли результаты наблюдения с высказанным предположением. При этом, если даже предположение о виде распределения сделано правильно, закон распределения наблюдаемой случайной величины будет отличаться от теоретического закона, т.к. число наблюдений ограничено.

Поэтому следует выяснить: является ли расхождение между статистическим и теоретическим законами распределения только следствием ограниченного числа наблюдений, или оно является чем-то более существенным.

Для решения этой задачи служит критерий согласия. Существует несколько видов критерия согласия: критерий согласия Пирсона, Колмогорова, Смирного, Фишера и т.д.

Для проверки гипотезы о законе распределения случайной величины применим критерий согласия Пирсона или c2.

1. Найдем число

Где- частота каждого интервала или разряда,

n– объем выборки (n= 100),

- теоретическая вероятность попадания случайной величины в iинтервал.

где, - границы интервалов.

- статистическое математическое ожидание,

- статистическое среднеквадратическое отклонение.

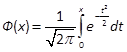- функция Лапласа.

Формула (4) следует из формулы вероятности попадания случайной величины Х, распределенной по нормальному закону, в интервал (a;b):

2. Определим число степеней свободы , где K– число интервалов или разрядов, 3 – число связей наложенных при выборе теоретического закона распределения. Связи:

1) Условие полноты ,

2) ,

3)

Замечание: частота miкаждого интервала должна быть не меньше 5 - 8, т.е. в этот интервал должно попадать не меньше 5 - 8 значений случайной величины. Если это не выполняется, то малочисленные интервалы следует объединить в один интервал или присоединить к соседнему, суммируя частоты.