Курсовая работа: Оценка параметрической надежности РЭС с использованием моделирования на ЭВМ постепенных отказов

1) Подсчитав по формуле (1.1) выходной параметр U_вых и установив допуск на выходной параметр DU_вых , смоделируем n РЭУ. РЭУ будем считать работоспособным, если значение его U_вых лежит в диапазоне установленного допуска т.е. U_вых ±DU_вых . Таким образом, нетрудно отыскать вероятность отсутствия параметрического отказа (см. раздел 2).

2) Воспользуемся гипотезой о том, что выходной параметр U_вых в течение времени t_зад часов распределен по нормальному закону. Замечено, что в большинстве случаев выходные параметры РЭУ хорошо описываются этим законом на всем участке от t=0 до t=t_зад . Однако в процессе эксплуатации, т.е. с изменением времени t, а также под воздействием дестабилизирующих факторов изменяются параметры нормального закона. Обычно происходит смещение среднего значения выходного параметра и изменяется степень его рассеивания относительного нового среднего значения. Здесь задачу оценки параметрической надежности сведем к отысканию плотности распределения изменений функционального параметра U_вых , и, предполагая нормальный закон распределения, к оценке его параметров, по которым затем определяем вероятность отсутствия параметрического отказа (см. раздел 2) [].

2. Выбор и обоснование метода решения задачи

Метод решения задачи состоит в следующем. Определяем выходной параметр по формуле (1.1) со значениям параметров элементов, не учитывая производственные допуска, корреляцию, воздействия температуры и времени. Назовем полученное таким образом напряжение “идеальным” - U_выхи . После чего задаемся допуском на выходной параметр DU_выхи , в пределах которого РЭУ считается исправным. Т.е. границы U_н и U_в фактически задаются нами, т.к. последние не указаны в задании. В программе этот диапазон задается в процентах, и, в последующем, пересчитывается в абсолютные величины, по которым и производятся сравнения. При анализе решаемой задачи мы задавились допусками 10%, 30% и 50%.

При помощи ЭВМ моделируем n различных реализаций РЭУ с параметрами элементов, распределенных по нормальному закону. Затем пересчитываем значения параметров элементов при воздействии на них дестабилизирующих факторов (в данном случае температуры) и времени. При этом предполагаем, что температурный коэффициенты a_R и a_U , а также коэффициенты старения С_R и С_U распределены по нормальному закону, а температура окружающей среды Т_раб - по равномерному. Так как закон распределения температуры окружающей среды был неизвестен, и не было возможности попытаться подобрать закон распределения экспериментально, то была принята гипотеза о том, что температура распределена по равномерному закону, ибо эта модель на практике является предельным наихудшим случаем разброса параметра. Определяем выходной параметр по формуле (1.1) - это напряжение назовем “реальным”.

По первому способу, изложенному в подразделе 1.2, вероятность отсутствия параметрического отказа определим следующим образом:

Р_пар (t_зад ) (U_н £U_выхр £U_в ) = , (2.1)

Где n_испр - число исправных РЭУ в момент времени t_зад ;

n- общее число смоделированных РЭУ;

U_н - нижняя граница исправной работы РЭУ U_н = U_выхи - DU_выхи ;

U_в - верхняя граница исправной работы РЭУ U_в = U_выхи + DU_выхи .

По второму способу, изложенному в подразделе 1.2, вероятность отсутствия параметрического отказа определим следующим образом.

Пусть случайное число x, имеющее нормальное распределение с параметрами m = m (x) и s = s (x), уже получено. Тогда для получения случайного числа z, имеющего нормальное распределение с параметрами m = m (z) и s = s (z) и коррелированного с x, необходимо произвести смещение параметров m = m (z) и s = s (z) с учётом коэффициента парной корреляции, а затем воспользоваться подпрограммой формирования случайных нормально распределённых чисел с параметрами m = m (z/x) и s = s (z/x):

(2.2)

(2.3)

Определяем математическое ожидание выходного параметра М* (U_выхр ) и его среднеквадратичное отклонение по формулам s* (U_выхр ):

М* (U_выхр ) = , (2.4)

s* (U_выхр ) = . (2.5)

Для определения точности и надежности полученных по формулам (2.4) и (2.5) оценок строим доверительные интервалы:

I_g = {M_н ; М_в } = . (2.6)

Так как мы воспользовались “правилом трех сигм”, то доверительный интервал гарантируется с вероятностью g=0,9973.

Определяем верхнюю и нижнюю допустимые границы U_выхр :

U_н = U_выхи - DU_выхи , (2.7)

U_в = U_выхи + DU_выхи . (2.8)

Так как мы воспользовались гипотезой о нормальном распределении выходного параметра, то искомую вероятность отсутствия параметрического отказа Р_пар (t_зад ) определим с помощью формулы:

Р_пар (t_зад ) (U_н £U£U_в ) =

= Ф (2.9)

Где M* (U_выхр /t=t_зад ) - математическое ожидание выходного параметра в момент времени t=t_зад ;

s* (U_выхр /t=t_зад ) - среднеквадратичное отклонение выходного параметра в момент времени t=t_зад [].

Графическая интерпретация формулы (2.9) приведена на рисунке (2.1).

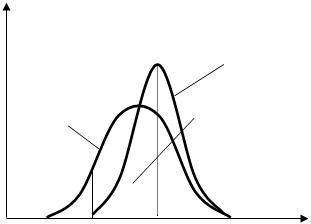w (U_вых )