Курсовая работа: Оценка тягово-скоростных свойств автомобиля КАМАЗ 43105

Удельное значение свободной силы тяги, равное отношению , называется динамическим фактором по тяге:

. (11)

При умножении всех членов уравнения (10) на выражение получается уравнение мощностного баланса автомобиля:

, (12)

где – мощности сопротивления подъему, качению, воздуху, разгону, дороге, кВт;

– тяговая мощность, подводимая к ведущим колесам, кВт.

С помощью уравнений силового и мощностного балансов можно находить все оценочные параметры тягово-скоростных свойств. Уравнения (10) и (12) являются дифференциальными уравнениями первого порядка с коэффициентами, нелинейно зависящими от скорости v и ее первой производной j . Так как отсутствуют точные выражения N_e = f ( n ), то и решение этих уравнений в общем виде затруднительно.

Для выхода из этого положения были разработаны аналитические и графические методы решения уравнений силового и мощностного балансов.

2.4 Подготовка исходных данных для определения скоростных и тягово-динамических характеристик

Для шины 1220х400–533 из источника [1] находят, что наружный диаметр колеса D=1200±10 мм, свободный радиус мм, статический радиус мм.

На дороге с твердым покрытием можно считать м.

Кинематический радиус качения колеса находят по формуле (13):

м. (13)

Далее принимают следующие значения коэффициентов и параметров:

– коэффициент коррекции ;

– коэффициент, учитывающий влияние скорости движения, k_f =6∙10^-6 ;

– коэффициент обтекаемости k_в =0,6 Н∙с² /м⁴ ;

– лобовая площадь автомобиля м² ,

где В – колея автомобиля, м;

Н_г – габаритная высота, м;

– фактор обтекаемости Н∙с² /м² ;

– коэффициент сопротивления качению радиальной шины 1220х400–533 при небольшой скорости движения ;

– продольный уклон дороги ;

– коэффициент суммарного сопротивления дороги

; (14)

– сила сопротивления дороги

. (15)

Свободная сила тяги определяется выражением:

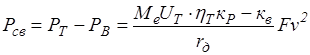, (16)