Курсовая работа: Побудова споживчої функції. Оцінка параметрів системи економетричних рівнянь

Таблиця 1.4 – Таблиця аналізу дисперсій стосовно даних задачі

Компоненти дисперсії	Число ступенів свободи,	Сума квадратів,	Середнє значення суми квадратів,
Регресія	1,00	43324,40	43324,40
Відхилення від регресії	10,00	1813,85	181,39
Всього	11,00	45138,25

, (1.24)

. (1.25)

Таким чином :

, (1.26)

де (1,10) – число ступенів свободи відповідно чисельника і знаменника.

. (1.27)

Висновок: > , 238,85 > 4,96 тобто розходження обґрунтованої та необґрунтованої складових дисперсії носить не випадковий характер і взаємозв’язок між рівнем споживання та рівнем доходу тісний.

Оцінку лінійного коефіцієнту кореляції здійснимо за допомогою формули [1]:

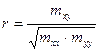, (1.28)

. (1.29)

Висновок: Високий лінійний коефіцієнт кореляції свідчить про тісний взаємозв’язок між роздрібним товарообігом та рівнем доходу .

Побудуємо довірчі інтервали для та . Побудова довірчого інтервалу для кутового коефіцієнту кореляції здійснюється за формулою:

, (1.30)

де – деяка похибка при оцінці ; – довірчий коефіцієнт при рівні імовірності та ступенях свободи. Знаходиться за таблицями –розподілу Ст’юдента .

Приймається якісна гіпотеза , відповідно до якої . Формула для розрахунку має вигляд [1]:

, (1.31)

(1.32)

; (1.33)

; (1.34)

. (1.35)

Висновок: Результати регресії не відповідають якісній гіпотезі, згідно до якої 0‹β‹1, тому робимо висновок про недостатню точність оцінки b.

Побудова довірчого інтервалу для коефіцієнта здійснюється за формулою [1]:

, (1.36)

де – деяка похибка при оцінюванні а ;

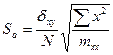, (1.37)

.(1.38)

; (1.39)

(1.40)