Курсовая работа: Полином Жегалкина

2) Метод неопределенных коэффициентов

- искомый полином Жегалкина (реализующий функцию ).

Вектор из формулы (1) будем называть вектором коэффициентов полинома .

Нам нужно найти неизвестные коэффициенты .

Поступаем так. Для каждого составим уравнение , где - выражение, получаемое из (1) при . Это дает систему из уравнений с неизвестными, она имеет единственное решение. Решив систему, находим коэффициенты полинома .

3) Метод, базирующийся на преобразовании вектора значения функции

Пусть - вектор значений функции.

Разбиваем вектор на двумерные наборы:

.

Операция T определена следующим образом:

.

Применяем операцию Т к двумерным наборам:

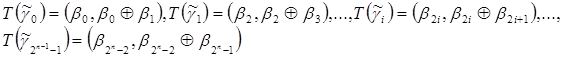
Используя построенные наборы, конструируем четырехмерные наборы, которые получаются в результате применения операции Т к четырехмерным наборам, выделяемым из.

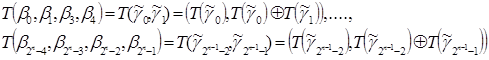
Затем от четырехмерных наборов переходим (аналогично) к восьмимерным и т.д., пока не построим - мерный набор. Он и будет искомым вектором коэффициентов полинома .

Пример:

Пусть вектор значений функций = (0,0,0,1,0,1,1,1)

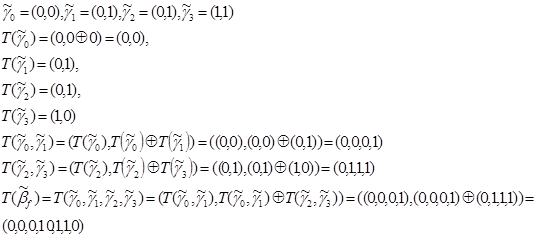
Полученный вектор является искомым векторов коэффициентов полинома .

Определение 2: Пусть M – некоторое подмножество функций из P2. Замыканием M называется множество всех булевых функций, представимых в виде формул через функции множества M. Обозначается [M].

Замечание. Замыкание инвариантно относительно операций введения и удаления фиктивных переменных.

Примеры.

1) M=P2, [M]=P2.

2) M={1,x1Åx2}, [M] – множество L всех линейных функций вида

, (ciÎ{0,1}).

Свойства замыкания:

1) Если М замкнуто, то [M]=M;

2) [[M]]=[M];