Курсовая работа: Полином Жегалкина
4) [M1ÈM2]Ê[M1]È[M1].
Определение 3. Класс (множество) M называется (функционально) замкнутым, если [M]=M.
Примеры.
1) Класс M=P2 функционально замкнут;
2) Класс {1,x1Åx2} не замкнут;
3) Класс L замкнут (линейное выражение, составленное из линейных выражений линейно).
Новое определение полноты. M – полная система, если [M]=P2.
Алгоритм
булевой функция полином жигалкин
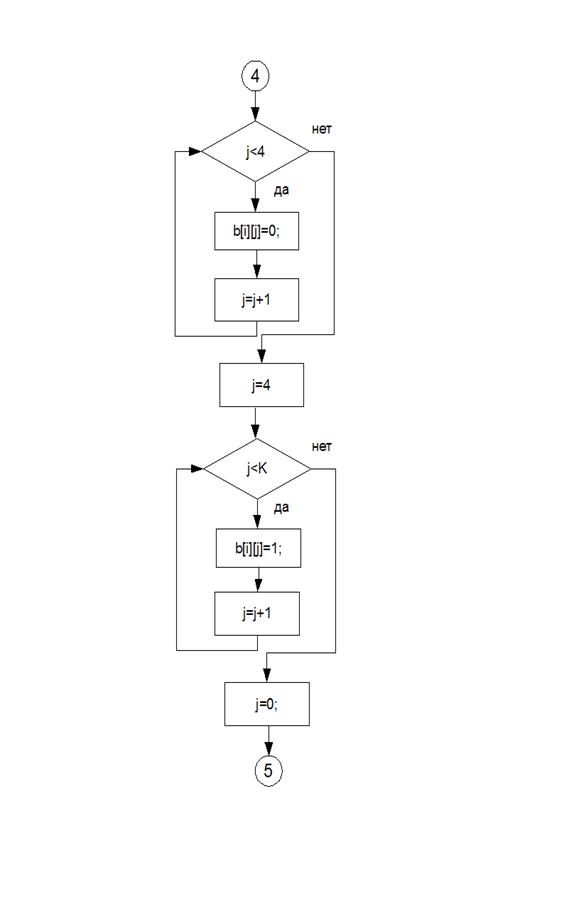
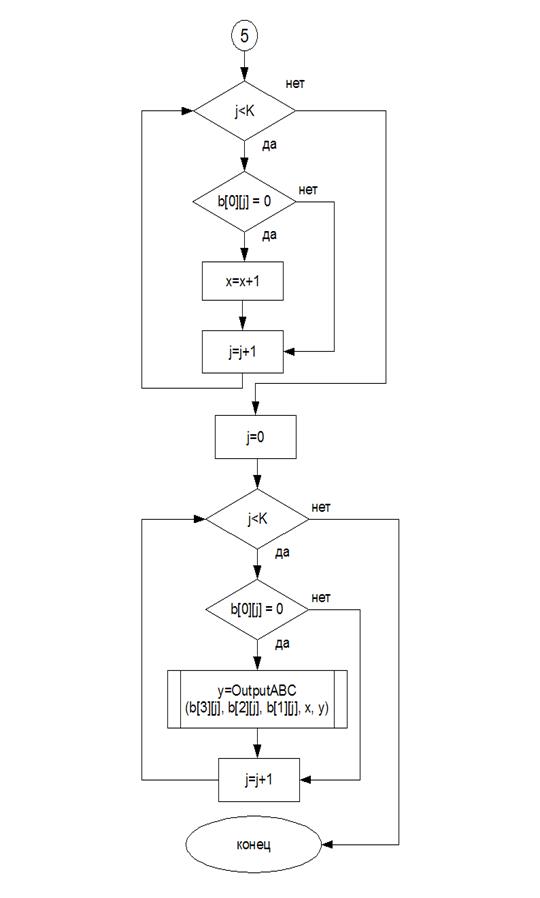
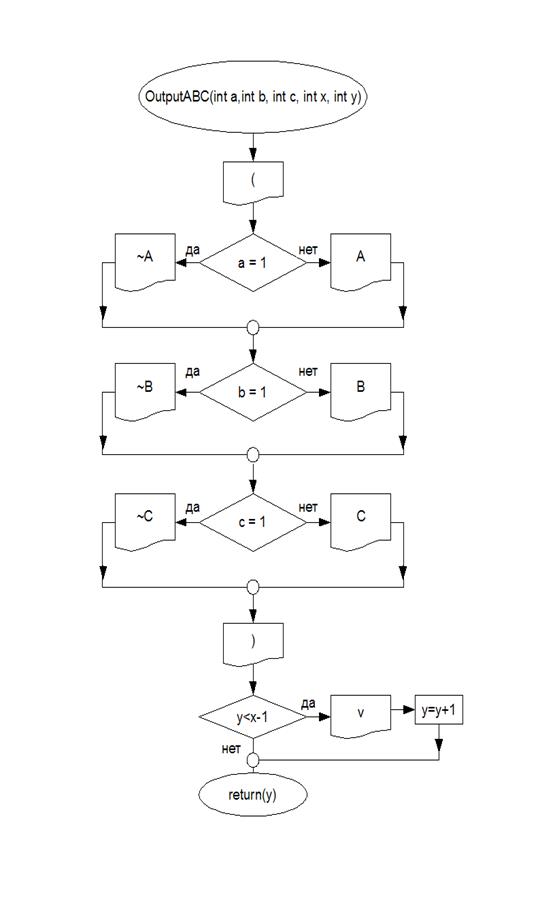
В данной программе был реализован метод неопределенных коэффициентов для построения полинома Жегалкина.
1. Получить таблицу истинности для определенного количества переменных;
2. Заполнить значения функции для каждого из наборов таблицы истинности;
3. Последовательно вычислить неизвестные коэффициенты;
4. Записать функцию в виде полинома Жегалкина с вычисленными коэффициентами.
| x1 | x2 | x3 | f |
| 0 | 0 | 0 | f1 |
| 0 | 0 | 1 | f2 |
| 0 | 1 | 0 | f3 |
| 0 | 1 | 1 | f4 |
| 1 | 0 | 0 | f5 |
| 1 | 0 | 1 | f6 |
| 1 | 1 | 0 | f7 |
| 1 | 1 | 1 | f8 |
![]() .
.
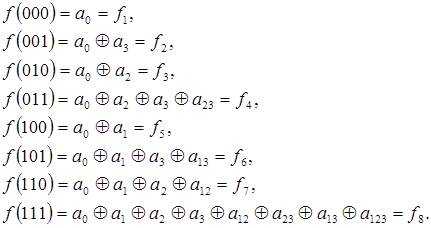
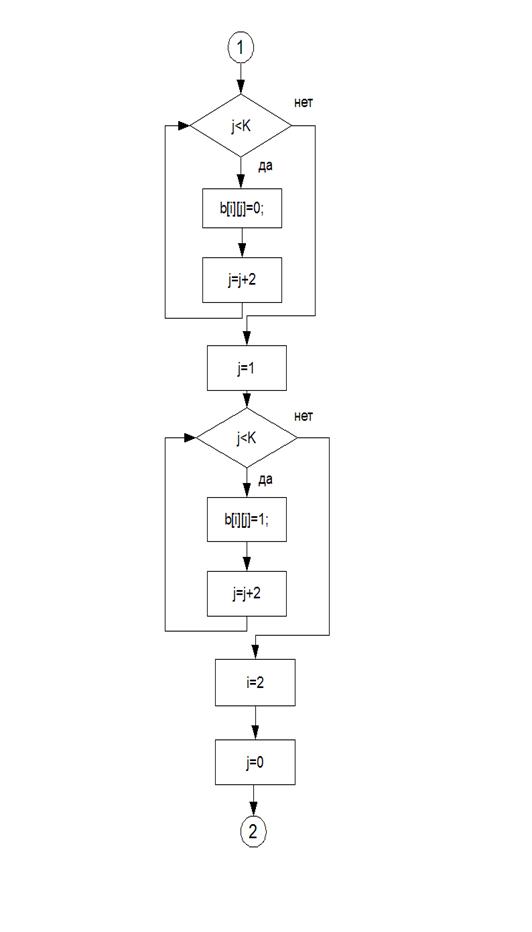
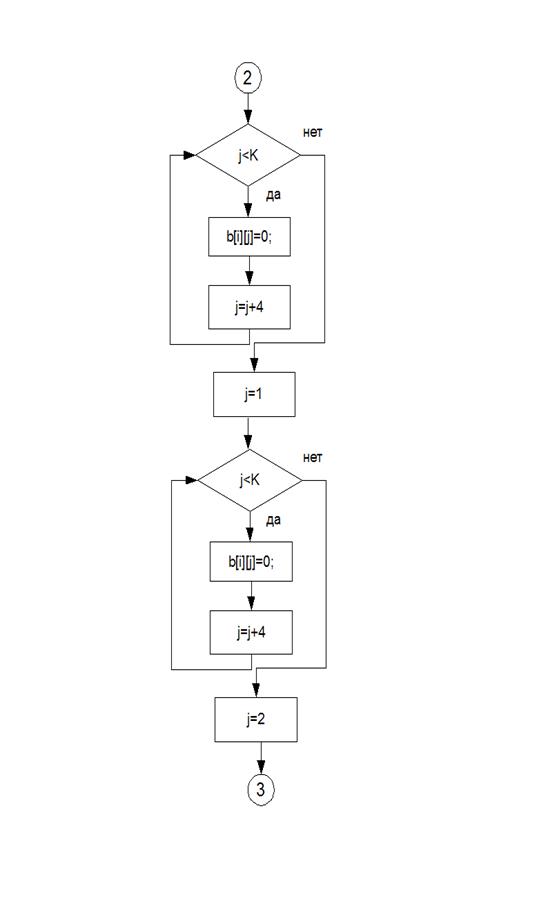
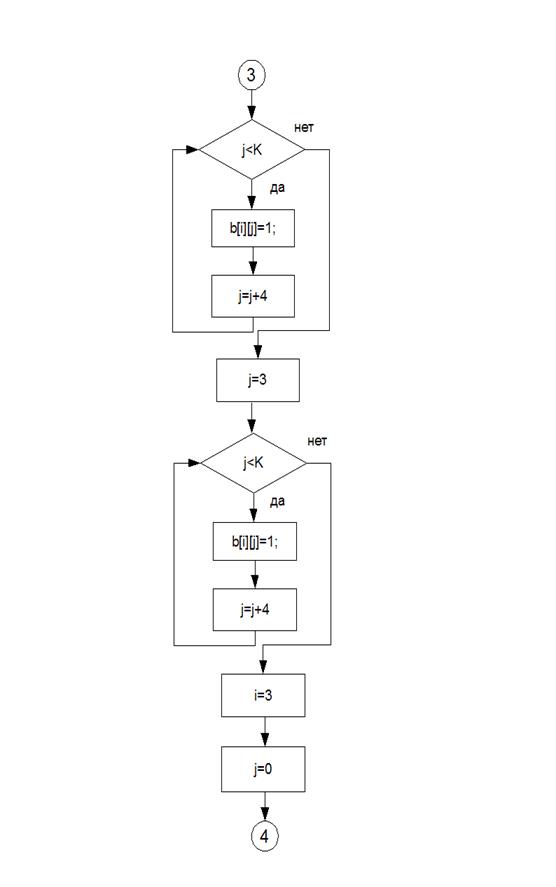
Листингпрограммы:
#include<iostream.h>
#include<conio.h>
int FuncVolume (int &f)
{
do {cout <<"Vvedite znachenit funkcii na dannom nabore :"<<endl;
cin>>f;