Курсовая работа: Полином Жегалкина

cout<<" 0 0 0 "<<f[0]

<<"\n 0 0 1 "<<f[1]

<<"\n 0 1 0 "<<f[2]

<<"\n 0 1 1 "<<f[3]

<<"\n 1 0 0 "<<f[4]

<<"\n 1 0 1 "<<f[5]

<<"\n 1 1 0 "<<f[6]

<<"\n 1 1 1 "<<f[7]<<"\n\n";

cout<<"\n\nZnachenie koefficientov v polimome Jigalkina : \n\n" ;

for (i=0; i<N;i++)

{

cout<<"a_"<<i<<" "<<a[i]<<"\n";}

cout<<"Polinom Jigalkina dlya dannoy funkcii imeet vid : \n f = "<<a[0]

<<"^("<<a[1]<<"*x_1)^("<<a[2]<<"*x_2)^("<<a[3]<<"*x_3)^("<<a[4]<<"*x_1*x_2)^\n^("<<a[5]<<"*x_2*x_3)^("<<a[6]<<"*x_1*x_3)^("

<<a[7]<<"*x_1*x_2*x_3)";

getch();

}

Тестирование программы:

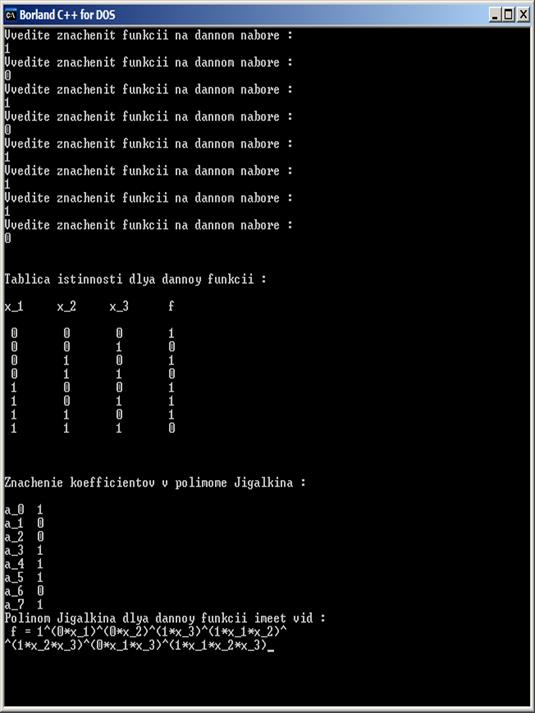
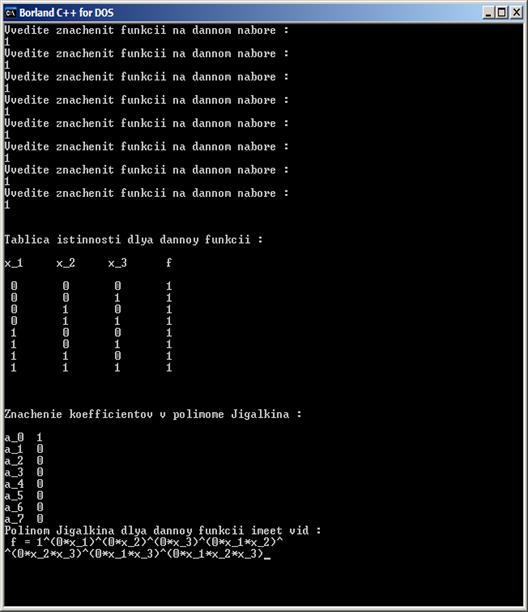
На каждом наборе вводятся единицы, то есть функция является тождественной единицей. Простейшая проверка на правильность работы программы:

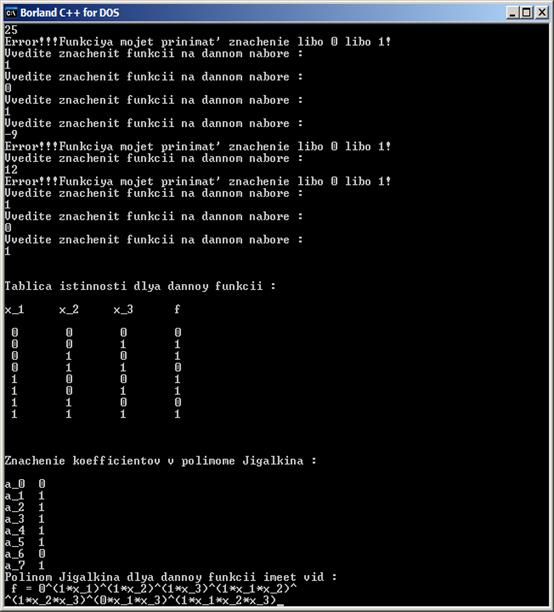
Так же реализована проверка на правильный ввод данных:

Заключение

В курсовой работе был реализован метод неопределенных коэффициентов для представления функции в виде полинома Жегалкина. По данному алгоритму на языке С++ была написана программа, результат которой был продемонстрирован.

Список использованной литературы

1. Яблонский С.В. Введение в дискретную математику. — М.: Наука. — 1986

2. Н.А.Ахметова, З.М.Усманова Дискретная Математика. Функции алгебры логики учебное электронное издание – Уфа – 2004

3. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике: Учебное пособие. – 3-е изд., перераб. – М.: ФИЗМАТЛИТ, 2005.