Курсовая работа: Повторные и независимые испытания. Теорема Бернулли о частоте вероятности

По формуле Бернулли требуемая вероятность равна

.

№6. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Решение. Вероятность рождения девочки

, тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

,,

,.

Следовательно, искомая вероятность

.

№7. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.

Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - "появление нестандартной детали", его вероятность, тогда. Отсюда по формуле Бернулли находим

.

№8. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.

Решение. Вычисляем по формуле Бернулли:

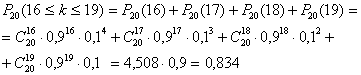
№9. Независимые испытания продолжаются до тех пор, пока событиеА не произойдетk раз. Найти вероятность того, что потребуетсяn испытаний (n і k), если в каждом из них.

Решение. СобытиеВ – ровноn испытаний доk -го появления событияА – есть произведение двух следующий событий:

D – вn -ом испытанииА произошло;

С – в первых( n –1) -ом испытанияхА появилось(к-1) раз.

Теорема умножения и формула Бернулли дают требуемую вероятность:

.

№10. Из n аккумуляторов за год хранения k выходит из строя. Наудачу выбирают m аккумуляторов. Определить вероятность того, что среди них l исправных. n = 100, k = 7, m = 5, l = 3.

Решение: Имеем схему Бернулли с параметрами p=7/100=0,07 (вероятность того, что аккумулятор выйдет из строя), n = 5 (число испытаний), k = 5-3 =2 (число "успехов", неисправных аккумуляторов). Будем использовать формулу Бернулли (вероятность того, что в n испытаниях событие произойдет k раз).

Получаем

№11. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут: а) три элемента; б) не менее четырех элементов; в) хотя бы один элемент.

Решение: Имеем схему Бернулли с параметрами p = 0,2 (вероятность того, что элемент откажет), n = 5 (число испытаний, то есть число элементов), k (число "успехов", отказавших элементов). Будем использовать формулу Бернулли (вероятность того, что для n элементов отказ произойдет в k элементах):. Получаем а)- вероятность того, что откажут ровно три элемента из пяти. б)- вероятность того, что откажут не менее четырех элементов из пяти (то есть или четыре, или пять). в)- вероятность того, что откажет хотя бы один элемент (нашли через вероятность противоположного события - ни один элемент не откажет).