Курсовая работа: Повторные и независимые испытания. Теорема Бернулли о частоте вероятности

.

Таким образом получили формулу:

.

Примеры

№17. Вероятность изготовления негодной детали равна 0,0002. Найти вероятность того, что среди 10000 деталей только 2 детали будут негодными.

Решение. n=10000; k=2; p=0,0002.

Искомая вероятность

.

№18. Вероятность изготовления бракованной детали равна 0,0004. Найти вероятность того, что среди 1000 деталей только 5 детали будут бракованными.

Решение. n=1000; k=5; p=0,0004.

Искомая вероятность

.

№19. Вероятность выигрыша лотереи равна 0,0001. Найти вероятность того, что из 5000 попыток выиграть удастся 3 раза.

Решение. n=5000; k=3; p=0,0001.

Искомая вероятность

.

5. Теорема Бернулли о частоте вероятности

Теорема. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа , приближенно равна удвоенной функции Лапласа при :

.

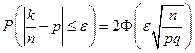Доказательство. Будем считать, что производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p. Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты от постоянной вероятности p по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства

. (*)

Заменим неравенство (*) ему равносильными:

.

Умножая эти неравенства на положительный множитель , получим неравенства, равносильные исходному:

.

Тогда вероятность найдем следующим образом:

.