Курсовая работа: Преобразование случайных сигналов в безынерционных нелинейных и инерционных линейных цепях
Пусть N = 200 ![]() = 9,8 mXN 0 = -1,1533 XN 0 = 0,7572
= 9,8 mXN 0 = -1,1533 XN 0 = 0,7572
Пусть N = 300 ![]() = 10,6 mXN 0 = -1,1803 XN 0 = 0,7569
= 10,6 mXN 0 = -1,1803 XN 0 = 0,7569
Пусть N = 400 ![]() = 8,8 mXN 0 = -1,2014 XN 0 = 0,7597
= 8,8 mXN 0 = -1,2014 XN 0 = 0,7597
Пусть N = 500 ![]() = 6,68 mXN 0 = -1,2082 XN 0 = 0,7452
= 6,68 mXN 0 = -1,2082 XN 0 = 0,7452
Пусть N = 600 ![]() = 8,07 mXN 0 = -1,2143 XN 0 = 0,7416
= 8,07 mXN 0 = -1,2143 XN 0 = 0,7416
Пусть N = 700 ![]() = 6,4 mXN 0 = -1,2196 XN 0 = 0,7471
= 6,4 mXN 0 = -1,2196 XN 0 = 0,7471
Пусть N = 800 ![]() = 5,77 mXN 0 = -1,2368 XN 0 = 0,7443
= 5,77 mXN 0 = -1,2368 XN 0 = 0,7443
Пусть N = 900 ![]() = 7,51 mXN 0 = -1,2265 XN 0 = 0,7480
= 7,51 mXN 0 = -1,2265 XN 0 = 0,7480
Пусть N = 1000 ![]() = 7,48 mXN 0 = -1,2119 XN 0 = 0,7473
= 7,48 mXN 0 = -1,2119 XN 0 = 0,7473
В дальнейшей работе будем использовать объем выработки N = 100, т. к. критерий Пирсона имеет наименьшее значение.


3. Энергетический спектр случайного сигнала Wx () показывает, как средняя мощность сигнала распределена по диапазону частот. Для большинства случайных сигналов ширина спектра теоретически бесконечно велика. Для оценки реальной ширины спектра вводят понятие эффективной ширины спектр э , которую можно определить как полосу частот, в пределах которой спектральная плотность средней мощности падает не более чем в 2 раза по сравнению с максимумом.
Корреляционная функция случайного процесса Rх () является внутренней мерой связанности процесса в различные моменты времени, отстоящие на , его свойства (помнить) предшествующие состояния следует интервал корреляции – это величина временного сдвига , начиная с которого значения сигнала X(t) и X(t+) могут считаться несвязанными.
Оценку величин интервала корреляции процесса к при известной корреляционной функции Rх () можно следующим образом: если процесс широкополосный, то к равен координате первого нуля функции Rх (); если процесс узкополосный, то к определяют по координате первого нуля огибающей функции Rх (). Корреляционная функция Rх () и энергетический спектр случайного сигнала Wx () связана между собой преобразованиями Фурье. Если реализация случайного процесса X(t) задана в виде выборочной последовательности значений Xi , где i= 1,2,3, … N, то
![]() , 0 k N1
, 0 k N1
где N1 – число отсчетов корреляционной функции и энергетического спектра (на 1 2 порядка меньше числа отсчетов сигнала N);
Т – интервал дискретизации сигнала.
= 2Пf = ![]() - шаг отсчета по частоте.
- шаг отсчета по частоте.
Корреляционная функция Rх (t) и энергетический спектр Wx (f) исходного сигнала изображены на рисунках (см. ниже). Это широкополосный сигнал. Т = 0.0004с; N1 = 10;
![]()
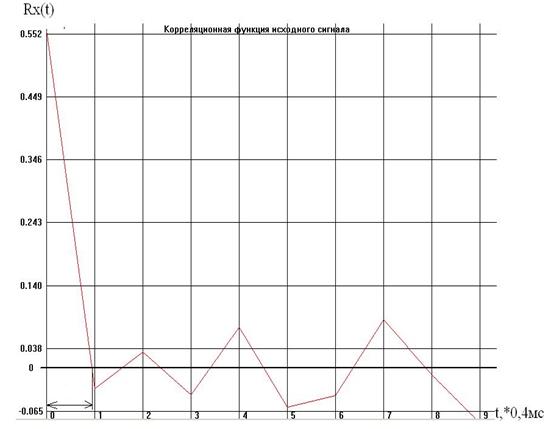

По графику корреляции видно что исследуется широкополосный сигнал, его интервал корреляции:
![]()
Энергетическая ширина спектра
![]()
4. Найдем P(x) для равномерного закона распределения
![]()