Курсовая работа: Преобразование случайных сигналов в безынерционных нелинейных и инерционных линейных цепях

Если во всей области изменения переменной Х связь отклика Y с воздействием Х, обусловленная видом характеристики y = f(x) нелинейного элемента, однозначна, то плотность вероятности распределения мгновенных значений P(y) по известной P(x) можно найти

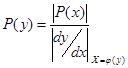
где преобразованная зависимость y = f(x).

Если нелинейность такова, что какому-то значению y = y₁ отвечает конечное множество значений

, , … , то

++ …

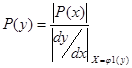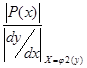Если линейность такова, что есть значения Y, которым в силу характеристики y = f(x) отвечает бесконечное число значений Х, то применяют следующее правило

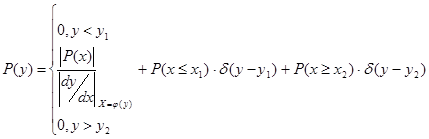
[-2,525; 0,042] [0, 3] P(x) = 0,39

У нас нелинейность вида

Y =

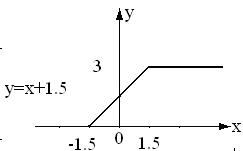
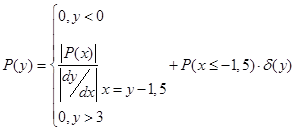
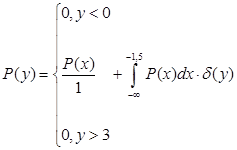
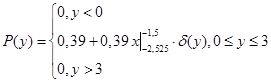
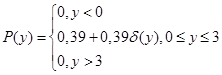
В результате преобразования случайного процесса X(n) в безынерционной нелинейной цепи мы получили новый сигнал Y(n).

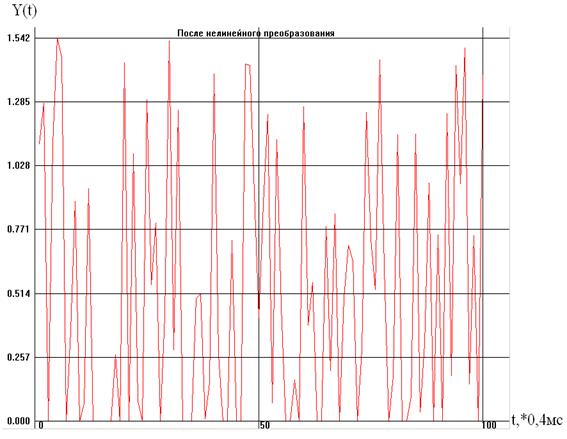
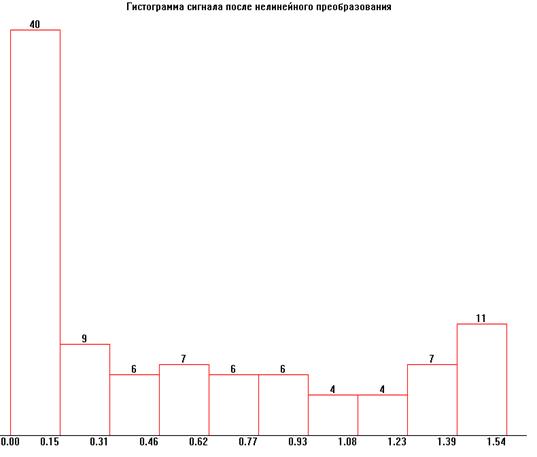
Для него m_{1 YN 0} = 0,5132 _{1 YN 0} = 0,5323 Гистограмма изображена на рисунке, ее огибающая схожа с графиком теоретически построенной функции P(y) следовательно, теоретические расчеты совпадают с практическим преобразованием.

Корреляционная функция R_y (t) и энергетический спектр случайного сигнала W_y (f) представлены на рисунках, приведенных ниже:

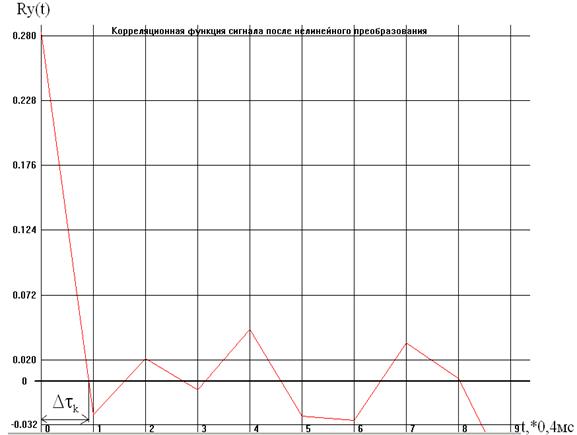
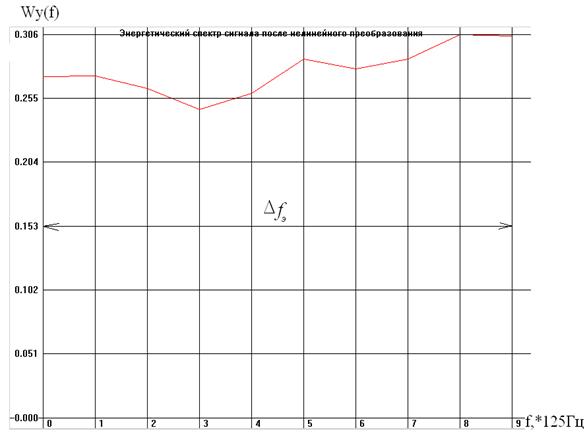
Интервал корреляции:

Энергетическая ширина спектра:

В результате преобразования случайного процесса X(n) в безынерционной нелинейной цепи случайный сигнал перестал быть равномерным. Математическое ожидание увеличилось и стало больше нуля. Среднеквадратичное отклонение уменьшилось примерно в 1,5 раза. Сигнал остался широкополосным.

6. В общем случае точно установить взаимосвязь закона распределения воздействия с законом распределения отклика линейной цепи и ее частотной характеристикой очень сложно. Но если протяженность во времени импульсной характеристики цепи такова, что хотя бы в несколько раз превышает _к входного случайного процесса, или полоса пропускания цепи в частотной области хотя бы в несколько раз меньше ширины энергетического спектра входного процесса, то при любом законе распределения P(х) входного процесса, случайный процесс на выходе линейной цепи будет иметь распределение, близкое к нормальному.

В результате фильтрации случайного процесса Y(n) в инерционной цепи (ПФ, f0 = 500 Гц, Q = 3) мы получили новый сигнал Z(n).