Курсовая работа: Преобразование случайных сигналов в безынерционных нелинейных и инерционных линейных цепях
Для него m1 ZN 0 = 0,0018 1 ZN 0 = 0,1679
Определим по гистограмме с помощью критерия 2 произошла ли нормализация случайного процесса Y(n) в результате его фильтрации в линейной цепи
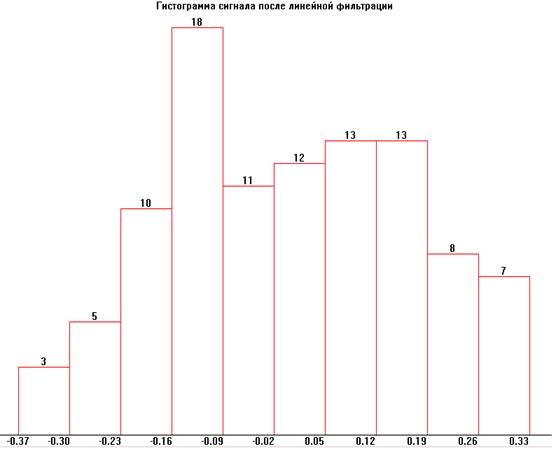
где nk – число отсчетов сигнала, попавший в k – интервал.
- теоретическая вероятность пребывания случайного сигнала в пределах каждого из интервалов X, N - общее число исследуемых отсчетов сигнала Ni = 10
P
=Ф(-1,8)-Ф(-2,21)= - 0,92814+0,97289=0,045
Р
=Ф(-1,38)+Ф(1,8)=-0,83241+0,92814=0,096
Р
=-Ф(0,96)+Ф(1,38)= -0,66294+0,83241=0,1694
Р
=-Ф(0,55)+Ф(0,96)= -0,41768+0,66294=0,24526
Р
=-Ф(0,13)+Ф(0,55)=-0,10348+0,41768=0,3142
Р
=Ф(0,29)+Ф(0,13)=0,22818+0,10348=0,33166
Р
=Ф(0,7)-Ф(0,29)=0,51608-0,22818=0,28789
Р
=Ф(1,12)-Ф(0,7)=0,73729-0,51607=0,22122
Р9=Ф(1,54)-Ф(1,12)=0,87644-0,73729=0,13915
Р10=Ф(1,95)-Ф(1,54)=0,94882-0,87644=0,07
| K | Pk | nk |  |
| 1 | 0,045 | 3 | 4,9 |
| 2 | 0,0096 | 5 | 2,5 |
| 3 | 0,1694 | 10 | 0 |
| 4 | 0,24526 | 18 | 6,4 |
| 5 | 0,3142 | 11 | 0,1 |
| 6 | 0,33166 | 12 | 0,4 |
| 7 | 0,28789 | 13 | 0,9 |
| 8 | 0,22122 | 13 | 0,9 |
| 9 | 0,13915 | 8 | 0,4 |
| 10 | 0,07 | 7 | 0,9 |
2 =17,4 Нормализация Р случайного процесса Y(n) в результате его фильтрации в линейной цепи не происходит.
Графики корреляционной функции и энергетического спектра представлены ниже:
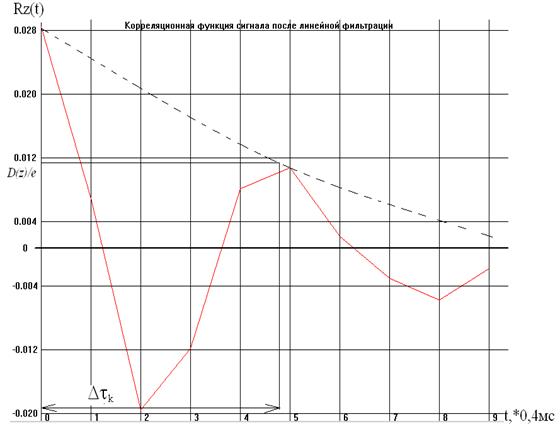
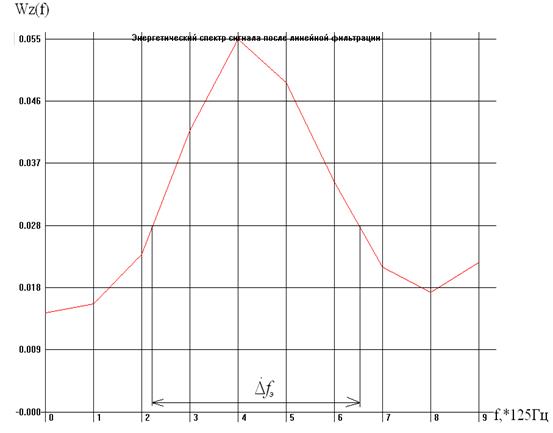
Интервал корреляции: 
Энергетическая ширина спектра: 
В результате фильтрации случайного процесса Y(n) в инерционной линейной цепи случайный сигнал становится близким к нормальному. К этому заключению приходим из того, что полоса пропускания цепи в частотной области почти в 2 раза меньше ширины энергетического спектра входного процесса. Математическое ожидание стало равно 0, 0018, а среднеквадратическое отклонение уменьшилось до 0,1679. Сигнал стал узкополосным – это произошло из-за частотной характеристики К() линейной цепи – ПФ.
Выводы
1. При взятой длине реализации N = 100, 2 является наименьшим из всех рассмотренных N. Математическое ожидание отличается на 9% от заданного, а среднеквадратическое отклонение на 1%
2. По виду корреляционной функции и энергетическому спектру заключаем, что сигнал широкополосный.
3. В результате преобразования случайного процесса X(n) в безинерционной нелинейной цепи, случайный сигнал перестал быть равномерным. Математическое ожидание увеличилось и стало больше 0, среднеквадратичное отклонение уменьшилось примерно в 1,5 раза. Сигнал остался широкополосным, к и fэ остались прежними.
4. В результате фильтрации случайного процесса Y(n) в инерционной цепи нормализация не произошла. Математическое ожидание стало равным 0,0018, а среднеквадратическое отклонение 0,1679. Сигнал стал узкополосным, энергетическая ширина спектра составила