Курсовая работа: Приемы финансового управления и принятия решений
Затраты на производство продукции,
тыс. руб.
· Принцип сопоставления валового дохода с валовыми издержками
Фирме следует осуществлять производство в краткосрочном периоде, если она может получить либо экономическую прибыль, либо убыток, который меньше, чем ее постоянные издержки. При этом ей необходимо производить такой объем продукции, при котором она максимизирует прибыли или минимизирует убытки.
Таблица 2.10. Сопоставление валового дохода с валовыми издержками
| Месяц года | Объемы производств, тыс. усл. ед. (Q) | Цена реализации, руб. (P) | Валовые издержки, тыс. руб. (P*Q=ТС) | Валовый доход, тыс. руб. (ТR) | Экономическая прибыль (убыток), тыс. руб. |
| 1 | 39 | 166 | 3940 | 6474 | 2534 |
| 2 | 55 | 141 | 5650 | 7755 | 2105 |
| 3 | 61 | 135 | 6020 | 8235 | 2215 |
| 4 | 62 | 134 | 6300 | 8308 | 2008 |
| 5 | 63 | 132 | 6350 | 8316 | 1966 |
| 6 | 79 | 104 | 7900 | 8216 | 316 |
| 7 | 65 | 123 | 6550 | 7995 | 1445 |
| 8 | 65 | 123 | 6600 | 7995 | 1395 |
| 9 | 70 | 118 | 7100 | 8260 | 1160 |
| 10 | 76 | 108 | 7750 | 8208 | 458 |
| 11 | 64 | 124 | 6600 | 7936 | 1336 |
| 12 | 65 | 123 | 6500 | 7995 | 1495 |
Таким образом, исходя из рассчитанной таблицы 2.10, мы можем сделать вывод, что предприятие, функционирующее в условиях заданных нами параметров, может варьировать объемы выпускаемой продукции в интервале от 39 до 65 единиц. Естественно, преследуя цель максимизации прибыли, на предприятии должны выбрать конкретный объем производства в определенном интервале. Данный объем соответствует максимальной разнице между показателями валового дохода и валовых издержек, в нашем примере равняется 46 единицам, при цене реализации равной 166 руб.
· Принцип сопоставления предельного дохода с предельными издержками
Предельный доход (MR) и предельные издержки (МС) показывают, сколько каждая дополнительная единица продукции будет добавлять к валовому доходу, с одной стороны, и к валовым издержкам — с другой. Иначе говоря, фирме следует сравнить предельный доход и предельные издержки каждой последующей единицы продукции. Любую единицу продукции, предельный доход от которой превышает ее предельные издержки, следует производить. Потому, что на каждой такой единице продукции фирма получает больше дохода от ее продажи, чем она прибавляет к издержкам, производя эту единицу. Следовательно, единица продукции добавляет к совокупным прибылям или — может быть и такой случай — уменьшает убытки. Точно так же, если предельные издержки единицы продукции превышают ее предельный доход, фирме следует снижать или приостанавливать производство этой единицы. Она добавит больше к издержкам, чем к доходу; такая единица продукции не будет окупаться.
Таблица 2.11. Сопоставление предельного дохода с предельными издержками
| Месяц года | Объемы производства, тыс. усл. ед. (Q) | Цена реализации, руб. (P) | Валовые издержки, тыс. руб. (P*Q) | Валовый доход, тыс. руб. (Z) | Предельный доход, тыс. руб. (MR) | Предельные издержки, тыс. руб. (MC) | Разница (MR-MC) |
| 1 | 39 | 166 | 3940 | 6474 | |||
| 2 | 55 | 141 | 5650 | 7755 | 80 | 107 | -27 |
| 3 | 61 | 135 | 6020 | 8235 | 80 | 62 | 18 |
| 4 | 62 | 134 | 6300 | 8308 | 73 | 280 | -207 |
| 5 | 63 | 132 | 6350 | 8316 | 8 | 50 | -42 |
| 6 | 79 | 104 | 7900 | 8216 | -6 | 97 | -103 |
| 7 | 65 | 123 | 6550 | 7995 | 16 | 96 | -81 |
| 8 | 65 | 123 | 6600 | 7995 | 0 | 0 | 0 |
| 9 | 70 | 118 | 7100 | 8260 | 53 | 100 | -47 |
| 10 | 76 | 108 | 7750 | 8208 | -9 | 108 | -117 |
| 11 | 64 | 124 | 6600 | 7936 | 23 | 96 | -73 |
| 12 | 65 | 123 | 6500 | 7995 | 59 | -100 | 159 |
В краткосрочном периоде выгодно производить то количество товаров, при котором предельные издержки ниже предельного дохода.
Фирма должна увеличивать свой выпуск до тех пор, пока предельные издержки не сравняются с предельным доходом.
В нашем примере вышеуказанному условию удовлетворяет выпуск продукции равный 61 единицам.
· Метод наименьших квадратов
Метод наименьших квадратов - статистический прием, с помощью которого неизвестные параметры модели оцениваются путем минимизации суммы квадратов отклонений действительных (эмпирических) значений от теоретических.
Метода наименьших квадратов заключается в выполнении следующих действий:
Для нахождения коэффициентов a и b: Для нахождения коэффициентов с и d:
![]()
![]()



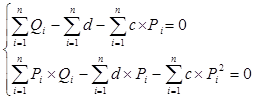


Произведём необходимые расчёты в таблице 2.12:
Таблица 2.12. Расчёт показателей для метода наименьших квадратов
| Месяц года | Q | P | P*Q | ||
| 1 | 39 | 166 | 6474 | 1521 | 27556 |
| 2 | 55 | 141 | 7755 | 3025 | 19881 |
| 3 | 61 | 135 | 8235 | 3721 | 18225 |
| 4 | 62 | 134 | 8308 | 3844 | 17956 |
| 5 | 63 | 132 | 8316 | 3969 | 17424 |
| 6 | 79 | 104 | 8216 | 6241 | 10816 |
| 7 | 65 | 123 | 7995 | 4225 | 15129 |
| 8 | 65 | 123 | 7995 | 4225 | 15129 |
| 9 | 70 | 118 | 8260 | 4900 | 13924 |
| 10 | 76 | 108 | 8208 | 5776 | 11664 |
| 11 | 64 | 124 | 7936 | 4096 | 15376 |
| 12 | 65 | 123 | 7995 | 4225 | 15129 |
| Итого: | 764 | 1531 | 95693 | 49768 | 198209 |
1. Найдём уравнение зависимости цены от объёма
Данное уравнение имеет следующий вид: ![]()




