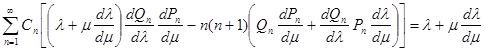Курсовая работа: Продольное и поперечное обтекание тел вращения

здесь последнее слагаемое представляет собой потенциал скоростей набегающего на тело однородного потока со скоростью на бесконечности V _¥ , направленной параллельно оси Оу (Приложение 1, б).

Полагая в только что выведенной общей формуле потенциала

A_n1 = с V _¥ С _n , A_n2 = A_n3 =… = 0, B_n1 = В_n2 =… = 0,

т.е. довольствуясь решением, содержащим cos e, и, кроме того, представляя у по формулам, помещенным в начале § 1, как функцию l, m и e

получим следующее выражение потенциала скоростей поперечно набегающего со скоростью V _¥ вдоль оси Оу потока:

или, используя определение присоединенных функций Лежандра (14),

(15)

Для определения постоянных С_n , как и ранее, следует составить граничное условие на заданной поверхности обтекаемого тела. В этом случае неосесимметричного движения функция тока отсутствует и приходится непосредственно вычислять нормальную скорость V_n = ¶ j / ¶ n и приравнивать ее нулю.

Несколько облегчая вычисления, выпишу в выбранной системе координат (l, m) условие, что при непроницаемости поверхности обтекаемого тела элемент дуги его меридианного сечения параллелен составляющей скорости в меридианной плоскости (условие скольжения жидкости по поверхности тела):

или, вспоминая выражения элементов дуг координатных линий и проекций градиента потенциала на направления этих линий,

Отсюда вытекает искомое граничное условие

(16)

в котором l является заданной функцией m согласно уравнению контура обтекаемого тела в меридиональной плоскости. Составляя частные производные ¶ j / ¶ l , ¶ j / ¶ m и используя (15) получаю:

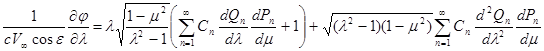
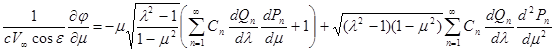
Заменив входящие сюда выражения вторых производных на основании дифференциальных уравнений функций Р_n и Q_n

получим после простых приведений

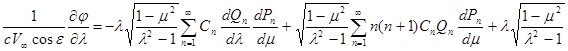
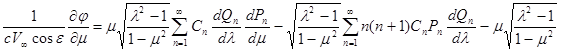
Подставляя эти выражения производных в (16) и используя ранее выведенные значения коэффициентов Ламе

получим после очевидных сокращений