Курсовая работа: Проектирование и исследование механизма крышкоделательной машины
Определим класса механизма. Для этого расчленим его на группы Ассура. Сначала отделяем группу Ассура II класса, образованную звеньями 4 и 5, затем отсоединяем группу Ассура II класса, образованную звеньями 2 и 3. остается ведущее звено и стойка 0, образующие механизм I класса.
Формула строения механизма I(0;1)®II(2;3)®II(4;5)
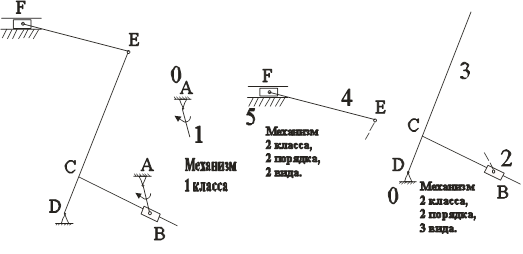
Класс присоединенных групп — второй, поэтому рассматриваемый механизм относится ко II классу.
2.3 Определение основных параметров и размеров
рычажного механизма.
Угловая скорость звена 1: ![]()
![]()
Размеры механизма заданны в задании:
lAB =0.22 м lCD =0.19 м lDE =0,86 м lEF =0,8 м X=0.8 м
Y1 =0.3 м Y2 =0.5 м
2.4 Описание определения кинематических характеристик рычажного механизма
2.4.1 Построение планов положений
Для построения планов положений механизма выбираем масштабный коэффициент ![]()
Тогда чертежные отрезки, изображающие звенья и расстояния на чертеже равны:
AB=lAB /mS =0.22/0.005=44 мм
CD=lCD /mS =0.19/0.005=38 мм
DE=lDE /mS =0.86/0.005=172 мм
EF=lEF /mS =0.8/0.005=160 мм
X=X/mS =0.8/0.005=160 мм
Y1 =Y1 /mS =0.3/0.005=60 мм
Y2 =Y2 /mS =0.5/0.005=100 мм
Делим траекторию движения точки B кривошипа на 12 равных частей и строим 12 положений механизма.. На всех звеньях показываем положения центров масс. Центры масс находятся посередине: AS1 =0 мм. Центр масс кулисы CB находится посередине максимальной длины звена, которую определим из построений.
2.4.2 Построение планов аналогов скоростей
Требуется построить 12 планов аналогов скоростей и определить длины отрезков, изображающих анализ скоростей на планах. Построение производим по группам Ассура в соответствии с формулой строения механизма I(0;1)®II(2;3)®II(4;5).
Поскольку между скоростями точек и аналогами скоростей существует пропорциональность, то для построения планов воспользуемся векторными уравнениями для построения планов скоростей.
Для построения планов аналогов скоростей механизма выбираем масштабный коэффициент ![]() ;
;
Переходим к построению плана аналога скоростей для группы Ассура (2;3’). Известна скорость точки B1 по величине и направлению. Скорость точки B3’ найдем, решив графически векторное уравнение:
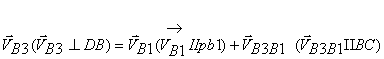 ;
;
Отрезок pb3 аналогичен скорости точки B3 . Для построения отрезка pс, изображающего аналог скорости точки С звена 3 воспользуемся теоремой подобия
![]() ;
;![]() ,
,
Направление ![]()
Скорости точек E и S3 найдём из соотношений