Курсовая работа: Прогнозирование функций по методу наименьших квадратов

Реферат

В отчете содержится: 24 формулы, 10 рисунков.

Ключевые слова: тренд прогноза, логнормальный закон, шум, критерий χ² -Пирсона, проверка гипотез, оценки расхождения.

Целью данной работы было исследование точности прогнозирования случайного процесса с использованием метода наименьших квадратов. Для этого проводился машинный эксперимент с использованием программы Mathcad 14. Основой для построения случайной функции являлась линейная функция, на которую был наложен случайный шум, распределенный по логнормальному закону с параметрами М[шума]=0 (математическое ожидание шума) и D[шума]=D (дисперсия шума). После чего полученная случайная функция аппроксимировалась линейным трендом, а также исследовалось расхождение между трендом и прогнозом с последующей оценкой близости распределения расхождений наблюдений и распределения сгенерированного шума по критерию χ² -Пирсона.

Определения и формулы

Математическим ожиданием P(ξ=x_i ) дискретной случайной величины ξ называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е:

, (1)

где х_i – значение случайной величины, p_i – вероятность этого значения, n – общее число значений.

Математическим ожиданием P(ξ=x_i ) непрерывной случайной величины ξ с плотностью распределения φ(x) называется число, определяемое равенством:

, (2)

где φ(x) – плотность распределения случайной величины.

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

(3)

Для непрерывной случайной величины формула (3) будет представлена в виде:

(4)

Среднее квадратичное отклонение(СКО) – это статистическая величина, описывающая разброс значений изучаемой величины вокруг ее ожидаемого значения:

(5)

В математической статистике оперируют оценками числовых характеристик, которые ищутся по случайной выборке. В отличие от самих параметров, оценки содержат элемент случайности. К оценкам параметров предъявляют определенные требования:

а) состоятельность – оценка, соответствующая этому требованию, с увеличением объема выборки сходится по вероятности к самому параметру;

б) несмещенность – математическое ожидание такой оценки равно оцениваемому параметру;

в) эффективность – дисперсия эффективной оценки минимальна.

Оценка математического ожидания ищется по формуле:

, (6)

где n – объем случайной выборки. Оценка, вычисленная по формуле (6), называется так же статистическим средним.

Оценка дисперсии вычисляется по формуле:

, (7)

где m – оценка математического ожидания случайной величины.

Оценка С.К.О. вычисляется по формуле:

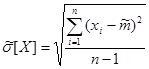, (8)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--