(18)

Условия минимума S будут равны для линейной функции:

(19)

(20)

Уравнения (19) и (20) можно записать в таком виде:

(21)

(22)

По уравнениям (21) и (22) легко найти a и b по опытным значениям x_i и y_i . Прямая (15), определяемая уравнениями (21) и (22), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (21) и (22), из которых определяется прямая (15), называются нормальными уравнениями.

Введение

В качестве тренда процесса был выбран линейный тренд вида

Y=at+b , (23)

где а =1, b =2. Тренд процесса показан на рисунке 3.

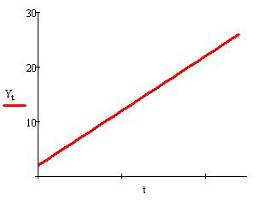
Рисунок 3. График тренда

График прямой с учетом сгенерированного шума по логнормальному закону выглядит так:.

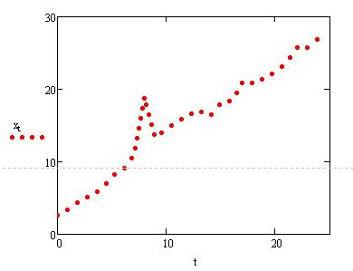
Рисунок 4. График прямой с учетом шума.

Наша задача в курсовом проекте заключается в определении насколько сильно шум влияет на прогнозирование. Для этого мы определяем расхождения между трендом и прогнозом и оцениваем степень расхождения из-за шума по критерию Пирсона

1. Построение прямой аппроксимирующей свойства тренда с помощью МНК

Наша ошибка сгенерирована по логнормальному закону с математическим ожиданием равным 0 и дисперсией равной 1. Гистограмма распределения шума представлена на рисунке 5.

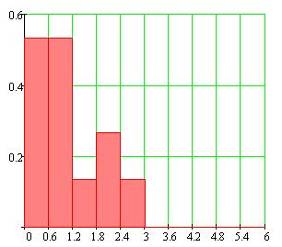
Рисунок 5. (Гистограмма распределения значений шума по интервалам).

С помощью формул (21) и (22) вычислим коэффициенты линейного уравнения тренда с учетом шума с помощью метода МНК:

По найденным коэффициентам строим график прямой, которая аппроксимирует основные свойства линейного тренда. График показан на рисунке 6:

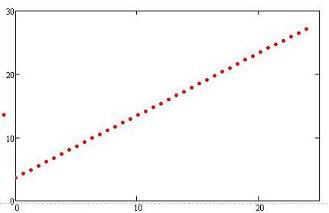
Рисунок 6. (Прямая, построенная по методу наименьших квадратов).

2. Прогнозирование дальнейшего продвижения тренда

Наша задача состоит в том, чтобы спрогнозировать дальнейшее поведение уравнения тренда и определить расхождения с спрогнозированными значениями.