Курсовая работа: Прогнозирование функций по методу наименьших квадратов

График расхождения исходного тренда и аппроксимированного тренда по МНК виден на рисунке 7. (Y_τ – исходный тренд; Z_τ – аппроксимированный тренд по МНК)

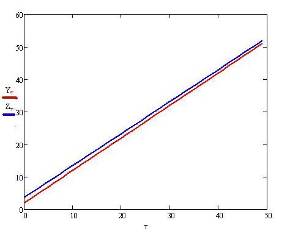
Рисунок 7 (На рисунке показаны тренд и аппроксимирующая его свойства прямая, построенная по методу наименьших квадратов).

Расхождения вычислены на удаленно отрезке(τ=50):

Δ= Z_τ - Y_τ =0.864

Проведем серию из 25 экспериментов по вычислению расхождений Δ по модулю:

N	1	2	3	4	5	6	7	8	9	10	11	12	13
Δ	0.661	0.673	0.756	2.366	0.488	3.569	0.864	5.651	2.328	0.851	1.259	1.718	0.618
N	14	15	16	17	18	19	20	21	22	23	24	25
Δ	3.765	0.502	3.762	1.369	2.185	0.494	1.851	0.067	2.012	4.429	3.441	0.601

Рассчитаем среднее значение Δ и среднеквадратичное отклонение по формулам (6) и (8):

Δср=1.851; σ=1.484

График на рисунке 8 отображает расхождения между исходной функцией и прямыми, полученными в результате аппроксимации по МНК. Синим цветом показаны полученные прямые, красным - исходная функция.

Рисунок 8. (На рисунке показаны тренд и несколько прямых, построенных по методу наименьших квадратов и аппроксимирующих свойства тренда).

3. Анализ результатов эксперимента

Полученные значения расхождений Δ представим в виде гистограммы и эмпирической функции по интервалам на рисунке 9:

Рисунок 9. (На рисунке представлены гистограмма распределения значений Δ по интервалам, а так же график функции распределения Δ).

Из рисунков видно, что закон Δ больше всего похож на логнормальный, поэтому для сравнения оценки расхождения распределения сгенерируем выборку объемом в 25 (а так же выборки объемом 100, 500 и 1500) по логнормальному закону с математическим ожиданием 0 и дисперсией 1 и вычислим параметры.

Сгенерированная выборка:

N	1	2	3	4	5	6	7	8	9	10	11	12	13
xL	3.532	0.494	1.002	3.027	2.441	0.055	0.116	1.229	0.54	0.302	1.104	2.161	1.358
N	14	15	16	17	18	19	20	21	22	23	24	25
xL	1.011	0.466	0.664	0.51	0.876	2.768	1.198	1.671	2.095	0.984	1.322	1.176

Оценки математического ожидания, дисперсии и СКО рассчитаем по формулам:

(24)

M[xL]=1.284; D[xL]=0.848; σ[xL]=0.921

На рисунке 10 показана гистограмма и эмпирическая функция по сгенерированной выборке:

Рисунок 10. (На рисунке показанная функций распределения, а так же гистограмма распределения значений по интервалам для случайной величины, распределенной по логнормальному закону распределения с выборкой 25).

4. Проверка близости по критерию χ2 Пирсона закона распределения расхождений наблюдений и сгенерированного шума

Проверим насколько расходятся значения при прогнозе и по тренду. Для этого определяются интервалы разбиения расхождений прогноза и вычисление вероятностей попасть в интервал по логнормальному закону с математическим ожиданием равным 0 и дисперсией 1 по формуле (9).

Далее посчитаем сумму квадратов расхождения между частотами и вероятностью попасть в интервал логнормального закона:

(25)

На основе суммы квадратов расхождения Δрасх можно посчитать расчетное значение критерия согласия Пирсона: