Курсовая работа: Прогнозирование функций по методу наименьших квадратов

При генерации шума мы используем два закона: нормальное и логнормальное распределение.

Нормальный закон: Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности:

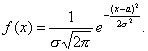(9)

Функция распределения F(x) в рассматриваемом случае принимает вид:

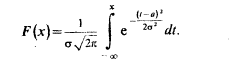(10)

График 1 – распределение плотности вероятности нормального закона:

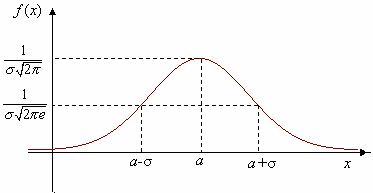
Рисунок 1. Плотность вероятности нормального закона

Говорят, что случайная величина X имеет логнормальное распределение с параметрами μ, σ, если X = exp(Y), где Y имеет нормальное распределение с параметрами μ, σ. Случайная величина с логнормальным распределением является непрерывной, и принимает только положительные значения. Графики плотности (привязан к левой вертикальной оси ординат) и функции (привязан к правой оси ординат) логнормального распределения с параметрами μ = 0, σ = 0.7 приведен на следующем рисунке 2:

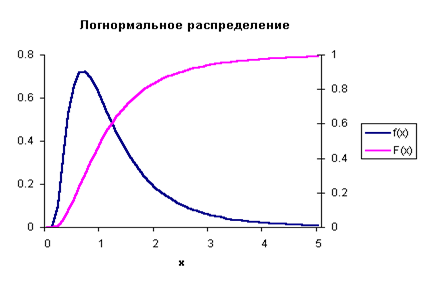
Рисунок 2. Логнормальное распределение

Плотность распределения логнормального закона:

(11)

Функция распределения:

(12)

Для определения степени расхождения теоретической кривой и статистических данных пользуются критериями согласия. Наиболее часто для проверки гипотезы о законе распределения используются 2 критерия: критерий λ-Колмогорова и критерий χ² -Пирсона.

Расчетное значение для критерия χ² -Пирсона вычисляется по формуле:

, где (13)

– (14)

вероятность попадания в интервал разбиения с номером i , m_i – число значений функции в интервале разбиения, m, σ – математическое ожидание и с.к.о. случайной величины X , Φ^* – интеграл вероятностей.

Чтобы определить функциональную зависимость между величинами по результатам наблюдений, используем метод наименьших квадратов (МНК):

Пусть из опыта получены точки:

x1, y1,

xn, yn

Требуется найти уравнение прямой y=ax+b (15), наилучшим образом согласующейся с опытными точками. Пусть мы нашли такую прямую. Обозначим через δ_i расстояние опытной точки от этой прямой (измеренное параллельно оси y).

Из уравнения (15) следует, что:

(16)

Чем меньше числа по абсолютной величине, тем лучше подобрана прямая (15). В качестве характеристики точности подбора прямой (15) можно принять сумму квадратов:

(17)