Курсовая работа: Работа с оптимизатором
В этом окне выбираем знак >= , а в правом окошке "Ограничение" ставим клавиатурой значение 0 (ноль). Вид окна примет, следующий вид:

То есть мы таким образом вводим ограничение Х1 ≥ 0, Х2 ≥ 0 из (1). Затем нажимаем кнопку "ОК" и тогда мы получим следующее окно:
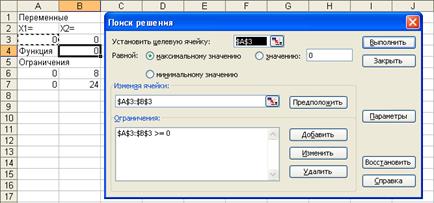
Далее, аналогично нажимая кнопку "Добавить" получим окно "Добавление ограничения", затем мышкой (не отпуская левую мышку) отмечаем ячейки А6 и А7. Потом отпуская мышку подводим курсор к окошку "Ограничение" и нажимая мышку ставим курсор в этой окошке. После чего мышкой отмечаем ячейки В6 и В7.
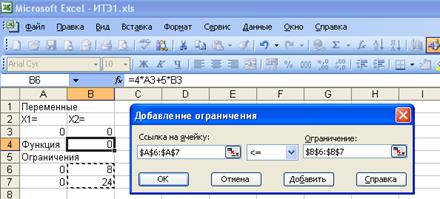
В этом окошке нажимая кнопку "ОК" добавляем это ограничение в окно оптимизатора:
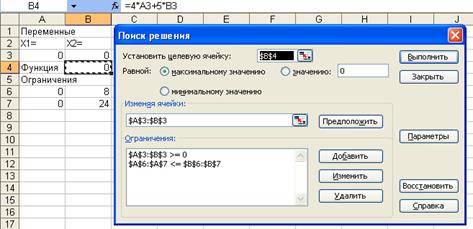
Теперь мы все ограничения (1) ввели в окно оптимизатора. Нажимая далее кнопку "Выполнить" получаем оптимальное решение заданной задачи:
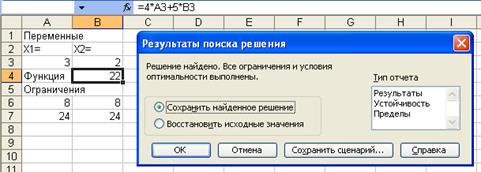
Из этого окна оптимизатора видно, что оптимальным решением являются Х1 =3, Х2 =2, при них достигается максимальное значение целевой функции Z=22.
Пример 2: Решение транспортной задачи с помощью оптимизатора. Математическая модель транспортной задачи сводится к минимизации линейной формы:
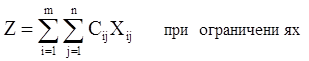
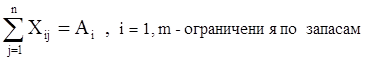

где С ij – стоимость доставки единицы груза из i-го пункта отправления в j-ый пункт назначения,
Х ij – количество единиц груза, запланированных к перевозке из i-го пункта в j-й,
А i - количество груза в i-том пункте отправления,
В j - количество груза в j-том пункте назначения.
Необходимым и достаточным условием разрешимости транспортной задачи является условие:
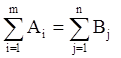
Математическая модель транспортной задачи относится к задачам линейного программирования и может быть решена симплексным методом. Рассмотрим транспортную задачу, матрица планирования которой имеет вид, представленный в таблице:
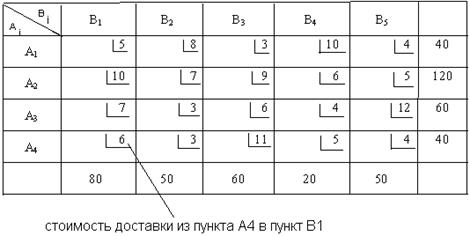
Решаем задачу с использованием программы Microsoft EXCEL. Для решения транспортной задачи с помощью оптимизатора «Поиск решения» введем данные как показано ниже на рисунке. Из рисунка видно, что вместо переменных Вj из вышестоящей таблицы используются имена столбцов EXCEL: A-E, а вместо переменных Аi используются номера строк от 1 и далее.
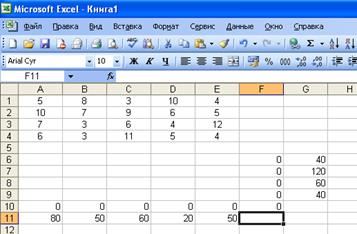
В ячейки А1:Е4 введем стоимость перевозок. Ячейки А6:Е9 отведены под значения объемов перевозок, пока неизвестных, но в этих ячейках после решения оптимизатора появятся оптимальный план перевозок. В ячейки G6:G9 введены объемы производства или запасы продукции на складах, а в ячейках А11:Е11 введены потребности (спрос) в продукции в пунктах потребления (или торговые точки).
В ячейку F10 вводится целевая функция: =СУММПРОИЗВ(А1:Е4; А6:Е9), как показано на след. рисунке:
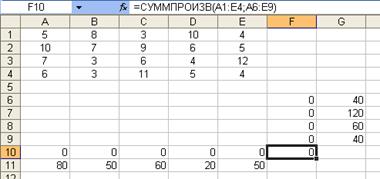
В ячейки А10:Е10 вводятся формулы: А10 → = СУММ (А6:А9)